로지스틱 사상

로지스틱 사상의 움직임을 거미줄 그림으로 나타낸 그림. 초기 조건을 0.2로 해 매개변수(그림의 r)을 1부터 4까지 늘렸을 때 일어나는 움직임의 변화가 애니메이션으로 나타난다.

로지스틱 사상(틀:Lang)이란 틀:수학라는 이차 함수의 차분 방정식(점화식)으로 정해진 이산역학계이다. 단순한 이차 함수의 식이면서 매우 복잡한 움직임을 내는 것으로 알려져 있다. 로지스틱 맵틀:Sfnm이나 이산형 로지스틱 방정식(틀:Lang)틀:Sfn, 단순히 이차 사상족틀:Sfn틀:Sfn이나 이차 함수족틀:Sfn라고도 불린다.

로지스틱 사상의 틀:수학 변수는 매개변수라 불리는 상수, 틀:수학 변수가 변수로, 적당히 틀:수학 변수의 값을 정하고 처음 틀:수학을 정해 계산하면 틀:수학라는 수열을 얻을 수 있다. 이 수열을 역학계 분야에서는 궤도라 부르고, 궤도는 틀:수학 변수에 어느 값을 주는가에 따라 변화한다. 매개변수 틀:수학 변수를 변화시키면 로지스틱 사상의 궤도는 하나의 값으로 떨어지거나, 몇 개의 값을 주기적으로 반복하거나, 혼돈이라 불리는 비주기적 변동을 보이거나 여러 모양으로 변화한다.

로지스틱 사상을 생물의 개체수를 나타내는 모델로 해 보는 입장에서는 변수 틀:수학 변수는 1세대, 2세대…라는 세대로 나타낸 개체수를 의미하고, 로지스틱 사상이란 현재의 개체수 틀:수학 변수로부터 다음 세대의 개체수 틀:수학를 계산하는 식이다. 생물 개체수 모델로의 로지스틱 사상은 어느 생물의 개체수가 어느 환경 안에서 생식하고, 더욱이 그 환경과 외부와의 사이에서 개체의 이출입이 없는 상황을 상정하고 있고, 틀:수학 변수는 정확히는 개체수 그 자체가 아닌, 그 환경 안에 존재 가능한 최대 개체수에 대한 비율을 의미한다. 미분방정식으로 개체수를 모델링하는 로지스틱 방정식의 이산화로부터도 로지스틱 사상은 유도 가능하고, '로지스틱 사상'이라는 이름도 그것에서 유래한다.

이차 함수의 역학계로의 연구는 20세기 초반부터 있었으나, 1970년대, 특히 수리생물학자 로버트 메이의 연구에 의해 로지스틱 사상은 널리 알려지게 됐다. 메이 이외에도 스타니스와프 울람과 존 폰 노이만, 틀:임시 링크, 틀:임시 링크, 틀:임시 링크, 미첼 파이겐바움 등이 로지스틱 사상의 움직임 해명에 관한 일을 하였다.

정의와 배경

단순히 말하면 로지스틱 사상이란 다음과 같은 이차 함수이다틀:Sfn.

식 안의 틀:수학 변수는 상수를 의미하고 매개변수라 불린다틀:Sfn. 틀:수학 변수 이외에는 틀:수학 변수나 틀:수학 변수이나 틀:수학 변수를 매개변수의 기호로 사용하는 경우도 있다틀:Sfnm.

식 (틀:EquationNote)에 대해 먼저 상수 틀:수학 변수의 구체적인 수치를 결정한다. 더욱이 변수 틀:수학 변수의 값을 적당히 정하고, 식에서 틀:수학 변수의 값을 계산한다. 그리고, 얻은 틀:수학 변수의 값을 새로운 틀:수학 변수의 값으로 보고 식을 대입해 새로운 틀:수학 변수의 값을 계산한다. 이러한 계산을 반복하는 것이 로지스틱 사상을 사용하는 것이다틀:Sfn. 예시로 틀:수학 변수를 틀:수학, 처음의 틀:수학 변수를 틀:수학로 했을 때의 반복 계산을 5회째까지 행하면 이하의 표처럼 된다틀:Sfn.

a를 2, 처음 x를 0.01로 했을 때 로지스틱 사상의 계산을 반복한 예시틀:Sfn
（소숫점 이하 10행까지로 계산）

계산 횟수	입력한 x의 값	y = 2x(1 − x)의 계산 결과
1	0.01	2 × 0.01 × (1 − 0.01) = 0.0198
2	0.0198	2 × 0.0198 × (1 − 0.0198) = 0.03881592
3	0.03881592	2 × 0.03881592 × (1 − 0.03881592) = 0.0746184887
4	0.0746184887	2 × 0.0746184887 × (1 − 0.0746184887) = 0.1381011397
5	0.1381011397	2 × 0.1381011397 × (1 − 0.1381011397) = 0.2380584298

로지스틱 사상 자체는 중학교에서 배우는 딱히 특별한 것 없는 이차 함수이고, 계산 자체도 중학생도 가능할 정도의 수준이다틀:Sfnm. 반복의 계산도 계산기로 가능하고, 컴퓨터의 스프레드시트를 사용하면 더욱 간단하게 가능하다틀:Sfn.

로지스틱 사상은 점화식 혹은 차분 방정식의 형식으로 다음과 같이도 쓸 수 있다틀:Sfnm.

틀:수학의 값을 정하면 이 차분 방정식에 따라 그 뒤의 변수의 값 틀:수학이 순차적으로 계산 가능하다틀:Sfn. 이러한 수열을 만드는 차분 방정식을 역학계(다이내미컬 시스템)이라고도 부른다틀:Sfn. 역학계란 시간과 함께 상태가 변화하는 계(시스템)으로, 특히 현재의 상태가 정해지면 그 후의 상태도 일의적으로 정해지는 계를 가리킨다틀:Sfn. 차분 방정식 (틀:EquationNote)과 같은 형식으로 정의된 역학계는 특히 이산 역학계라고 불린다틀:Sfn.

역학계적인 시점에서는 변수 틀:수학 변수의 밑첨자 틀:수학 변수을 시각이나 시간으로 부른다틀:Sfnm. 수열의 초기 조건 틀:수학은 초기 조건이라 불린다.틀:Sfn 변수의 시간 변화의 모습을 명확한 전문용어는 아니나, 움직임이라 부른다.틀:Sfn 그러나 시각 틀:수학 변수은 물리적인 시간을 정말로 의미하고 있는 것은 아니고, 어떠한 현상의 진행을 표시하고 있는 편의적인 레이블이다.틀:Sfn

나중에 후술하듯이, 로지스틱 사상은 생물의 개체수의 변화를 생각하는 식으로 세상에 알려진 측면을 가진다.틀:Sfn 이 경우, 틀:수학 변수는 어느 세대의 생물의 개체수를 서식 환경에서 가능한 최대 서식 개체수로 나눈 값을 의미하고 있다.틀:Sfn 차분 방정식(틀:EquationNote)에 의해 틀:수학 변수세대째의 개체수부터 틀:수학세대째의 개체수가 계산이 가능하다는 것이 생물 개체수 모델로의 로지스틱 사상의 의미이다.틀:Sfn 개체수가 증가하면 개체수의 증가 속도는 감소하는 것으로, 이 효과를 로시특 사상에서는 틀:수학라는 항으로 도입하고 있다.틀:Sfn 예를 들면, 어느 세대에서 개체수가 최대 서식 개체수에 가깝고, 틀:수학라고 하면 항 틀:수학는 틀:수학에 매우 가까운 수치로 되므로, 다음 세대의 개체수 틀:수학은 급격하게 감소하는 것으로 된다.틀:Sfn

'로지스틱 사상'의 이름에서 나오는 사상이란 어느 집합의 원소를 또 어느 집합의 원소에 대응시키는 규칙을 가리키는 용어이다.틀:Sfn 함수와 비슷한 것이나, 함수를 수 이외의 집합도 다루는 경우도 포함해 더욱 일반화한 것이 사상이라 할 수 있다. 사상이라는 시점에서는 로지스틱 사상은 실수의 한 점을 실수의 한 점으로 대응시키는 규칙이라고 할 수 있다.틀:Sfnm 단, '함수'와 '사상'에 수학 전체에서 공유되는 엄밀한 구분은 존재하지 않고, 실제로 어느 쪽의 말을 사용할지는 각 분야의 관습에 의한 것이 크다. 역학계 분야에서는 식 (틀:EquationNote)와 같은 차분 방정식을 사상으로 잡아 사상이라는 말로 부르는 경우도 많다.틀:Sfnm

로지스틱 사상을 사상의 형태로 표현하면

이나

와 같이 나온다.틀:Sfnm 사상이 매개변수 틀:수학 변수에 의존하고 있는 것을 명확히 하기 위해

와 같이 사상의 기호에 매개변수 기호의 첨자를 붙여 나타내는 경우도 있다.틀:Sfnm 식 (틀:EquationNote))이나 식 (틀:EquationNote)와 같은 사상으로의 표현은 식 (틀:EquationNote)와 같은 차분 방정식의 표현과 실질적으로 동등하나, 시각 틀:수학 변수을 하나하나 적지 않아도 되는 편리성도 있기에 종종 사용된다.틀:Sfn

이산 역학계의 수열 틀:수학은 사상 틀:수학 변수를 반복해 적용시켜 만들어낸다는 것으로도 볼 수 있다.틀:Sfnm 초기 조건을 틀:수학라고 하면

와 같이 수열은 틀:수학에 사상을 반복해 적용시켜 만들어진 것으로도 적을 수 있다.틀:Sfn 이와 같이 사상을 반복해 적용시키는 조작을 사상의 반복(iteration) 등으로 부른다.틀:Sfnm 간단하게 표기하기 위해 사상의 반복을

와 같이 적는다.틀:Sfn 틀:수학으로 틀:수학에 대한 틀:수학 변수의 틀:수학 변수회 반복을 의미하고 있다.틀:Sfn 그리고 차분 방정식으로부터 얻어지는

라는 열, 혹은 사상의 반복으로부터 얻어지는

라는 열을 역학계에서는 궤도라고 부른다.틀:Sfnm 역학계라는 분야의 관심은 주어진 역학계의 궤도의 움직임을 연구하는 것이다.

입력과 결과가 단순한 비례 관계로 이어져있는 시스템을 선형이라고 하고, 비례 관계로 나타내는 것이 불가능한 시스템을 비선형이라고 한다.틀:Sfn 로지스틱 사상은 생각할 수 있는 한 가장 단순한 비선형 함수인 2차 함수로 정의된다.틀:Sfnm 그러나 그 꽤나 간단한 식과는 정반대로 로지스틱 사상은 꽤나 복잡한 움직임을 만들어낸다.틀:Sfn 2차 함수의 반복 계산이라는 설정이 현대 수학의 주제의 하나로, 다양한 수학 이론을 야기한다.틀:Sfnm 후술하듯이 로지스틱 사상에서는 혼돈(카오스)이라는 현상이 나타나고, 혼돈 입문으로 적합한 제재이기도 하다.틀:Sfn

정의역과 그래프

로지스틱 사상의 그래프. (x_n+1과 x_n의 함수) 그래프는 포물선의 형태를 하고 있고, 매개변수 a가 변하면 포물선의 꼭짓점이 바뀐다.

전술했듯이, 로지스틱 사상에서는 생물의 개체수의 변동을 생각하는 모델로의 측면이 있다. 이때, 로지스틱 사상의 변수 틀:수학 변수는 생물의 개체수를 최대 서식지로 나눈 값이었으므로 틀:수학 변수가 취할 수 있는 수치는 틀:수학의 사이로 한정된다.틀:Sfn 그러한 사정도 있고, 로지스틱 사상의 변수의 범위를 닫힌구간 틀:Closed-closed로 한정해 그 움직임이 의논되는 경우가 많다.틀:Sfnm

변수를 항상 틀:수학으로 한정하려 하면 필연적으로 매개변수 틀:수학 변수가 취하는 범위는 틀:수학부터 틀:수학까지 틀:수학로 한정된다.틀:Sfn 왜냐하면, 틀:수학이 틀:Closed-closed의 범위 내에 있으면 틀:수학의 최댓값은 {{수학|틀:수직분수}로 된다.틀:Sfn 따라서 틀:수학에서는 틀:수학의 값이 틀:수학을 넘을 가능성이 나온다.틀:Sfn 한편, 틀:수학 변수가 음수일 때는 틀:수학 변수가 음의 값을 취하게 돼버린다.

사상의 그래프를 이용하는 것으로, 그 움직임의 대부분을 알 수도 있다.틀:Sfnm 로지스틱 사상 틀:수학의 그래프는 가로축을 틀:수학(혹은 틀:수학 변수)로 하고, 세로축을 틀:수학(혹은 틀:수학)로 해서 평면상에 틀:수학과 틀:수학의 관계를 나타낸 곡선이다.틀:Sfn 로지스틱 사상의 그래프는 틀:수학의 경우를 제외하고,

을 꼭짓점으로 하는 포물선의 형태를 하고 있다.틀:Sfnm 틀:수학 변수를 변화시키면 꼭짓점은 상하로 움직이고, 포물선은 형태를 바꾼다.틀:Sfn 또, 로지스틱 사상의 포물선은 가로축 (틀:수학의 직선)과 두 점에서 만난다.틀:Sfn 틀:수학과 틀:수학이 그 두 개의 교점으로 이들의 위치는 틀:수학 변수의 값에 영향을 받지 않고 일정하다.틀:Sfn

로지스틱 사상의 그래프 상에서 거미줄 그림에 따른 궤도를 그린 예시. 또, 그래프 상의 고정점 x_f 1, x_f 2의 위치.

사상의 그래프는 특히 로지스틱 사상과 같은 1 변수의 사상의 그래프는 그 사상의 움직임을 이해하기 위한 열쇠이다.틀:Sfn 그래프의 효과의 하나는 고정점이라 불리는 점의 표시이다.틀:Sfn 사상의 그래프에 겹쳐지듯이 틀:수학의 직선（45°의 직선）을 긋는다. 이 45° 직선과 그래프가 만나는 점이 있으면, 그 점이 고정점이다.틀:Sfnm 식으로 적으면 고정점은

을 만족하고 있는 점으로, 사상을 적용해도 변화하지 않는 점을 의미한다.틀:Sfnm 고정점을 틀:수학으로 표기하는 것으로 한다. 로지스틱 사상의 경우에 식 (틀:EquationNote)를 만족하는 고정점은 틀:수학를 풀어

의 두 점이다.（틀:Math의 경우를 제외한다.)틀:Sfnm 고정점의 개념은 이산 역학계에 있어 가장 중요하다.틀:Sfn

1 변수 사상에 대해 사용할 수 있는 또 하나의 그래프를 이용한 기술이 거미줄 그림(cobweb plot)으로 불리는 수법이다.틀:Sfn 가로축 위에 초기 조건 틀:수학을 정한 뒤 그곳에서 틀:수학의 곡선까지 세로 방향으로 직선을 긋는다. 틀:수학의 곡선과 만나는 곳애서 틀:수학의 45° 직선까지 가로 방향으로 직선을 긋고, 45° 직선에 만난 곳에서 틀:수학의 곡선까지 세로 방향으로 직선을 긋는다. 이를 반복하는 것으로, 평면 위에 거미줄상 내지 계단상의 그림이 나온다.틀:Sfn 사실 이 작도는 도시적으로 궤도의 계산하는 것과 마찬가지로, 작성된 거미줄상의 그림은 틀:수학에서 출발하는 궤도를 나타낸다.틀:Sfn 이 그림에 의해 궤도의 전체적인 움직임을 한 눈에 보는 것이 가능하다.틀:Sfn

움직임, 매개변수 a에 의한 변화

로지스틱 사상의 매개변수(그림에서는 r)가 0.02부터 4까지 변화될 때의 움직임의 변화를 나타낸 애니메이션. 가로축이 반복수 n（그림에서는 t）, 세로축이 x로, 반복 계산 200회까지의 x를 나타내고 있다.

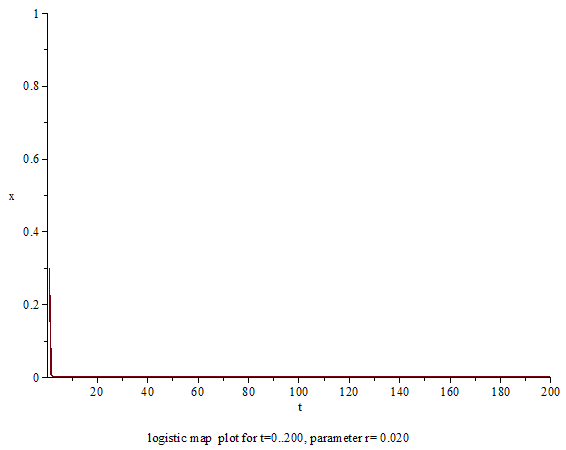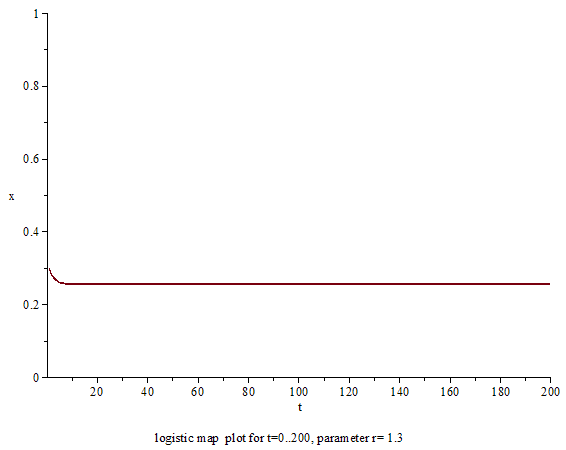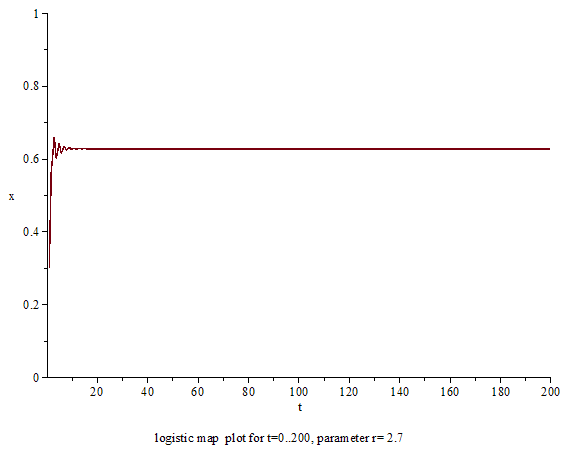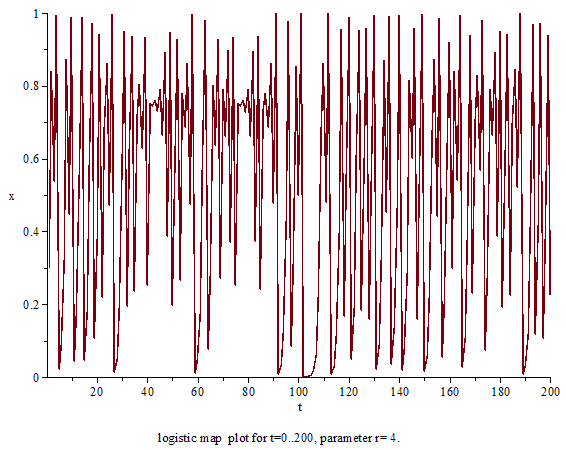
상술했듯이, 로지스틱 사상 자체는 어떠한 특별한 것 없는 2차 함수이고, 궤도의 계산 자체도 중학생이어도 가능할 정도이다.틀:Sfnm 역학계적으로 중요한 문제는 매개변수 틀:수학 변수를 변화시키면 궤도의 움직임이 어떻게 바뀌는가에 있다.틀:Sfn 틀:수학 변수의 수치에 따라, 로지스틱 사상의 궤도의 움직임은 단순하게도 복잡하게도 바뀐다.틀:Sfn 이하, 틀:수학 변수를 늘였을 때에 로지스틱 사상의 움직임이 어떤 식으로 변화해가는가를 순차적으로 설명한다.

0 ≤ a < 1의 경우

먼저, 매개변수가 틀:수학일 때는 초기 조건 틀:수학이 어떤 값이든 틀:수학으로 된다.틀:Sfn 결국, 틀:수학의 로지스틱 사상의 궤도는 초기 조건 이후의 값이 전부 틀:수학으로 되는 궤도로, 이 경우 별로 조사할 내용은 없다.틀:Sfn

다음으로, 매개변수가 틀:수학의 범위에 있을 때, 초기 조건 틀:수학이 틀:수학부터 틀:수학까지의 어떤 수치여도, 틀:수학 변수은 단조롭게 감소해간다.틀:Sfn 결국, 틀:수학의 극한으로 틀:수학 변수은 틀:수학으로 수렴한다.틀:Sfn 이 수렴한 틀:수학이라는 점은 식 (틀:EquationNote)으로 나타낸 고정점 틀:수학이다.틀:Sfn 이렇게 주변의 궤도가 수렴하는 타입의 고정점은 점근적 안정, 안정 혹은 흡인적이라고 불린다.틀:Sfnm 반대로 시간 틀:수학 변수의 증가와 함께 틀:수학의 부근의 궤도가 틀:수학로부터 떨어져간다면, 그 고정점 틀:수학는 불안정이나 반발적이라고 불린다.틀:Sfnm

매개변수 a = 0.9의 거미줄 그림(왼쪽）과 시계열(n과 x_n의 관계）의 그림（오른쪽). 궤도는 0을 향해 단조 감소로 수렴한다.

고정점이 점근적 안정인지 아닌지를 알기 위해서는 사상 틀:수학 변수의 미분을 구한다는 일반적으로 간단한 방법이 있다.틀:Sfn 틀:수학의 미분 틀:수학를 틀:수학로 나타내는 것이다. 이 미분이 고정점 틀:수학 변수로

이라는 조건을 만족시키면, 틀:수학 변수는 점근적 안정이다.틀:Sfn 여기서 틀:절댓값는 〇의 절댓값을 의미한다.

점근적 안정인 고정점（왼족）과 불안정한 고정점（오른쪽）의 접선의 기울기와 주위의 궤도의 모습

사상의 그래프에서 이러한 것을 보면, 그래프의 곡선 위의 점 틀:수학 변수의 접선의 기울기가 틀:수학에서 틀:수학의 사이에 있으면 틀:수학 변수는 안정으로, 그 주위의 궤도는 틀:수학 변수로 끌어당겨진다는 것이다.틀:Sfn 로지스틱 사상의 미분은

으로, 틀:수학 동시에 틀:수학에서는 틀:수학이므로 고정점 틀:수학은 식 (틀:EquationNote)을 만족하고 있다.틀:Sfn

단, 식 (틀:EquationNote)에 의한 판별법은 틀:수학 변수에서 어느 정도의 범위에 있는 궤도가 틀:수학 변수로 끌어당겨지는가는 알 수 없다.틀:Sfn 어디까지나 틀:수학 변수가 있는 근방 내의 틀:수학 변수가 수렴하는 것을 보증하고 있을 뿐이다.틀:Sfn 지금의 경우, 틀:수학으로 수렴하는 초기 조건의 구간은 닫힌구간 틀:Closed-closed 전역이나, 이를 명확히 알기 위해서는 다른 고찰을 필요로 한다.틀:Sfn

고정점이 불안정한지 아닌지의 판별 방법은 비슷하게 사상의 미분에서 알 수 있다.틀:Sfn 어느 고정점 틀:수학 변수가

를 만족할 때, 틀:수학 변수는 불안정하다.틀:Sfn 매개변수가 틀:수학의 범위에 있을 때에는 또 하나의 고정점 틀:수학는 음의 값이기에 닫힌구간 틀:Closed-closed의 범위에서는 나타나지 않지만, 불안정한 고정점으로 존재하고 있다.틀:Sfn

1 ≤ a ≤ 2의 경우

매개변수가 틀:수학일 때, 로지스틱 사상의 궤도는 여태까지와 비슷하게 틀:수학으로 수렴한다.틀:Sfn 단, 수렴하는 속도가 틀:수학에서는 천천히 된다.틀:Sfn 틀:수학의 고정점 틀:수학은 점근적 안정이기는 하나, 식 (틀:EquationNote)을 만족하지 않는다.틀:Sfn 실인즉, 식 (틀:EquationNote)에 의한 판별 방법은 사상을 고정점 근방에서 1차 근사하는 것에 따라 성립한다.틀:Sfn 틀:수학에서는 이 근사가 성립하지 않게 되고, 안정·불안정은 사상의 2차(제곱)의 항에 따라 결정되게 된다.틀:Sfn

틀:수학의 상태를 그래프로 보면 틀:수학에서 그래프의 곡선이 45° 대각성에 접한 상태로 된다.틀:Sfn 이때, 틀:수학의 범위에서는 음의 점위로 존재했던 고정점 틀:수학의 값은 틀:수학으로 된다.틀:Sfn 결국, 틀:수학 변수가 증가함에 따라 틀:수학의 값은 틀:수학에 가까워지고, 틀:수학에서 틀:수학는 틀:수학과 충돌한다.틀:Sfn 이 충돌에 의해 넘김고비 갈림(혹은 제한이동 분기, 초월 임계 분기)(Transcritical bifurcation)라는 현상이 일어난다.틀:Sfn

a = 1에서 일어나는 로지스틱 사상의 넘김고비 갈림의 모습. a < 1에서는 x_f 2가 불안정한 고정점으로 [0, 1]의 밖에 존재하고 있으나, a = 1에서 두 개의 고정점이 충돌하고, a > 1에서는 x_f 2가 안정적인 고정점으로 [0, 1]의 사이에서 나타난다.

분기란 역학계의 움직임이 정성적으로 변하는 현상을 가리키는 용어로, 이 경우의 넘김고비 갈림에서는 고정점끼리 안정성의 교체가 일어난다.틀:Sfn 결국, 틀:수학 변수가 틀:수학 미만에서는 틀:수학은 안정, 틀:수학는 불안정에 해당했으나, 틀:수학 변수가 틀:수학을 넘으면 틀:수학은 불안정, 틀:수학는 안정적으로 된다.틀:Sfn 분기가 일어날 때의 매개변수의 값은 분기점이라고 불린다.틀:Sfn 여기서는 틀:수학이 분기점이다.틀:Sfn

분기의 결과, 로지스틱 사상의 궤도는 틀:수학이 아닌 틀:수학로 수렴하게 된다.틀:Sfnm 상세하게 말하면, 매개변수가 틀:수학라면 틀:수학과 틀:수학을 제외한 열린구간 틀:Open-open 위의 값에서 출발하는 궤도는 단조 증가 혹은 단조 감소하면서 틀:수학으로 수렴한다.틀:Sfnm 수렴의 방법의 차이는 초기 조건이 어느 범위에 있는가에 따른다.틀:Sfn 틀:수학에서는 단조 증가로 수렴하고, 틀:수학에서는 단조 감소로 수렴하며, 틀:Math에서는 처음 한 단계를 제외하고 단조 증가로 수렴한다.틀:Sfn

또, 분기에 따라 고정점 틀:수학은 불안정화하지만, 틀:수학 이후도 고정점으로 계속 존재한다.틀:Sfn 이 불안정 고정점 틀:수학에 이르는 초기 조건이 틀:수학 자신 이외에 존재하지 않는 것은 아니다.틀:Sfn 그것이 틀:수학로, 틀:수학 변수의 값에 관계 없이 로지스틱 사상은 틀:수학을 만족하므로 틀:수학에서 사상을 1회 적용하면 틀:수학으로 된다.틀:Sfn 이 틀:수학과 같이 유한 번의 사상의 반복으로 고정점에 직접 다다르는 점은 최종적 고정점 등으로 불린다.틀:Sfn

2 < a < 3의 경우

a = 2.8의 거미줄 그림의 애니메이션. 고정점의 주변을 돌면서 수렴한다.

매개변수가 틀:수학의 경우는 초기 조건 틀:수학과 틀:수학을 제외하고, 틀:수학의 경우와 같이 고정점 틀:수학로 수렴한다.틀:Sfn 단, 이 경우는 단조로 수렴하는 것은 아니다.틀:Sfn 변수가 틀:수학으로 어느 정도 가까워지면 변수는 틀:수학보다 커지고 작아지고를 반복하고, 틀:수학의 주변에서 진동하면서 수렴해가는 궤도를 보인다.틀:Sfn

궤도의 고정점 주변에서의 진동은 다음과 같은 범위를 왔다갔다 한다. 이 매개변수 범위에서는 틀:수학는 열린구간 틀:Open-open 안에 존재한다.틀:Sfn 사상을 한 번 적용하면 틀:수학로 되는 값을 틀:수학로 표기한다. 즉, 틀:수학 라는 관계이다.틀:Sfnm 변수가 열린구간 틀:Open-open에 들어갔을 때, 궤도의 고정점 주변에서의 진동이 일어난다.틀:Sfn 열린구간 틀:Open-open는 반열린구간 틀:Open-closed로 되고, 반열린구간 틀:Open-closed는 반열린구간 틀:Closed-open의 안으로 대응되고…라는 식으로 진동한다.틀:Sfnm

일반적으로 분기의 모습을 이해하기에는 분기 다이어그램이 도움이 된다.틀:Sfn 이 그림은 고정점(또는 후술할 주기점(Periodic point)) 틀:수학 변수를 매개변수 틀:수학 변수의 함수로 나타낸 그래프로, 가로축으로 틀:수학 변수의 값을 취하고, 세로축으로 틀:수학 변수의 값을 취해 나타낸다.틀:Sfn 안정적인 고정점과 불안정한 고정점을 구별하기 위해 전자의 곡선은 실선으로 나타내고, 후자의 곡선은 점선으로 나타내거나 한다.틀:Sfn 로지스틱 사상의 분기 다이어그램을 그리면 고정점 틀:수학를 나타내는 직선과 고정점 틀:수학를 나타내는 곡선이 틀:수학과 접하면서 안정성이 교체되는 모습을 볼 수 있다.틀:Sfn

매개변수 0부터 3까지의 로지스틱 사상의 분기 다이어그램. 파란 선이 고정점 x_f 1 = 0을 나타내고, 빨간 선이 고정점 x_f 2 = 1 − 틀:수직분수를 나타낸다.

3 ≤ a < 3.44949…의 경우

매개변수가 틀:수학의 경우도 궤도는 고정점 틀:수학로 수렴한다.틀:Sfn 그러나, 틀:수학의 경우보다도 변수가 수렴하는 속도는 느리다.틀:Sfn 틀:수학에서는 미분계수 틀:수학는 틀:수학에 이르고, 식 (틀:EquationNote)을 만족하지 않게 된다.틀:Sfn 틀:수학 변수가 틀:수학을 넘으면 틀:수학로 되고, 틀:수학는 불안정한 고정점으로 된다.틀:Sfn 즉, 틀:수학으로 다시 분기가 일어난다.틀:Sfn

틀:수학에서는 주기배가 분기라고 불리는 종류의 분기가 일어난다.틀:Sfn 틀:수학부터는 궤도는 한 점으로 수렴하지 않게 되고, 충분한 시간 틀:수학 변수이 진행한 뒤에도 큰 값과 작은 값을 번갈아 계속 취하게 되는 움직임으로 변한다.틀:Sfn 예를 들면 틀:수학라면, 변수는 틀:수학과 틀:수학이라는 두 개의 값을 번갈아 계속해서 취한다.틀:Sfn

이와 같이 같은 값을 주기적으로 계속 도는 궤도를 주기 궤도라고 부른다.틀:Sfn 이 경우, 틀:수학의 변수의 최종적인 움직임은 두 주기의 주기 궤도이다.틀:Sfn 주기 궤도를 구성하는 하나하나의 값(점)을 주기점(Periodic point)이라고 부른다.틀:Sfn 틀:수학의 예로 말하면 틀:수학와 틀:수학이 각각 주기점이다.틀:Sfn 어느 틀:수학 변수가 주기점이라고 하면, 두 주기점의 경우는 틀:수학 변수에 사상을 2회 적용하면 본래로 돌아오므로

라는 관계가 성립한다.틀:Sfn 이 식에 로지스틱 사상의 식 (틀:EquationNote)을 적용하면

라는 4차 방정식을 얻을 수 있다.틀:Sfnm 이 방정식의 해가 주기점이다.틀:Sfnm 실은 고정점 틀:수학과 고정점 틀:수학 또한 식 (틀:EquationNote)를 만족한다.틀:Sfn 따라서, 식 (틀:EquationNote)의 해 중 두 개의 해는 틀:수학과 틀:수학에 상당하고, 남은 두 개의 해가 두 주기점이다.틀:Sfn 두 주기점을 각각 틀:수학로 나타낸다고 한다. 식 (틀:EquationNote)을 푸는 것으로 틀:수학를 다음과 같이 얻을 수 있다.틀:Sfnm

고정점의 안정성과 같은 것을 주기점에 대해서도 말할 수 있다.틀:Sfn 즉, 주위의 궤도를 끌어당기는 주기점은 점근적 안정적인 주기점으로 불리고, 주위의 궤도가 멀어지는 주기점은 불안정한 주기점이라고 불린다.틀:Sfn 주기점의 안정성 판별도 고정점과 같이 가능하다.틀:Sfn 일반적인 경우를 상정해 사상을 틀:수학 변수회 반복시킨 틀:수학에 대해 생각한다. 이 미분 틀:수학를 틀:수학라고 나타낸다고 한다. 어느 틀:수학 변수-주기점 틀:수학가

을 만족시키면 틀:수학는 점근적 안정이다.틀:Sfn 불안정에 대해서도 고정점과 같이

을 만족시키면 틀:수학는 불안정하다.틀:Sfn

이상의 주기점의 안정성의 논의도 고정점과 같이 그래프 묘사에 따라 이해하기 쉽게 된다.틀:Sfn 이 그림에서는 가로축 틀:수학 변수에 대해 세로축을 틀:수학로 하고, 틀:수학와 틀:수학 변수의 관계를 나타내는 곡선을 그린다.틀:Sfn 이 곡선과 45° 직선의 교점은 식 (틀:EquationNote)를 만족시키는 점이므로 교점은 고정점과 두 주기점을 나타내고 있다.틀:Sfn 로지스틱 사상의 틀:수학의 그래프를 그리면 고정점 틀:수학에서의 접선의 기울기는 틀:수학을 경계로 1을 넘어 불안정화하는 것이 관찰 가능하다.틀:Sfn 동시에 새로운 두 개의 교점이 나타나고, 이들이 주기점 틀:수학과 틀:수학이다.틀:Sfn

두 주기점의 미분계수를 로지스틱 사상에 대해 실제로 계산하면

로 된다.틀:Sfn 이를 식 (틀:EquationNote)에 대입하면 매개변수 틀:수학 변수가

을 만족했을 때에 두 주기점이 점근적 안정이라는 것을 알 수 있다.틀:Sfn 이 범위는 틀:수학으로 되고, 즉 틀:수학 변수가 틀:수학를 넘으면 두 주기점은 점근적 안정이 아니게 되며, 다시 움직임이 바뀐다.틀:Sfn

닫힌구간 틀:Closed-closed 안의 거의 전체의 초기 조건이 두 주기점에 끌어당겨지나, 틀:수학과 틀:수학도 닫힌구간 틀:Closed-closed 안으로 불안정한 고정점으로 계속 남아있는다.틀:Sfn 이들 불안정 고정점은 이후 틀:수학 변수를 계속 증가시켜도 닫힌구간 틀:Closed-closed 안에 계속 남아있는다.틀:Sfn 이로 인해 초기 조건이 틀:수학 또는 틀:수학일 때는, 궤도가 두 주기점으로는 끌어당겨지지 않는다.틀:Sfn 더욱이 초기 조건이 틀:수학에 대한 최종적 고정점인 경우와 틀:수학에 대한 최종적 고정점일 경우도 궤도는 두 주기점으로는 끌어당겨지지 않는다.틀:Sfn 이러한 최종적 고정점인 점은 닫힌구간 틀:Closed-closed의 안에 무한히 존재한다.틀:Sfn 그러나, 이러한 점의 수는 닫힌구간 틀:Closed-closed이라는 실수의 집합과 비교하면 매우 작다.틀:Sfn

3.44949… ≤ a ≤ 3.56994…의 경우

매개변수 틀:수학 변수가 틀:수학를 넘으면 여태까지 안정적이었던 두 주기점이 불안정하게 되고, 안정적인 네 주기점이 새로 생겨나 궤도는 네 주기의 진동으로 끌어당겨지게 된다.틀:Sfnm 즉, 틀:수학에서 다시 주기배가 분기가 일어난다.틀:Sfn 네 주기점의 틀:수학 변수의 값도

을 만족하므로 이 식을 풀면 네 주기점의 틀:수학 변수의 값을 구하는 것이 가능하다.틀:Sfn 단, 식 (틀:EquationNote)은 16차 방정식이고, 고정점과 두 주기점의 네 개의 해를 묶어낸다고 해도 12차 방정식이다.틀:Sfn 이로 인해, 이를 풀고 두 주기점과 같이 네 주기점의 값을 나타내는 틀:수학 변수의 양함수를 얻는 것은 불가능하다.틀:Sfn

256주기까지의 분기점의 예시틀:Sfn

k번째의 분기	주기 2k	분기점 ak
1	2	3.0000000
2	4	3.4494896
3	8	3.5440903
4	16	3.5644073
5	32	3.5687594
6	64	3.5696916
7	128	3.5698913
8	256	3.5699340

더욱이 틀:수학 변수가 커지면 안정적인 네 주기점은 다시 주기배가 분기를 일으키고, 안정적인 여덟 주기점이 생긴다.틀:Sfn 이후, 틀:수학 변수가 증가함에 따라 16주기, 32주기, 64주기…로 주기배가 분기가 무한하게 계속 일어나며, 최종적으로는 무한 주기 즉 영원히 전의 값으로 돌아갈 수 없는 궤도로 된다.틀:Sfn 이 주기배가 분기의 무한의 계열은 캐스케이드(cascade)라고 불린다.틀:Sfn 이 주기배가 분기는 무한하게 일어나지만 한편, 주기배가 분기가 발생하는 틀:수학 변수의 간격은 등비수열적으로 감소한다.틀:Sfn 이로 인해 매개변수 틀:수학 변수가 어느 유한한 값에 이를 때까지 주기배가 분기의 무한 번의 발생이 일어난다.틀:Sfn 틀:수학에서 일어난 1주기부터 2주기로의 분기를 첫 번째 주기배가 분기로 센다고 한다. 그러면 이 주기배가 분기의 캐스케이드 안에서는 틀:수학 변수번째의 분기점에서 안정적인 틀:수학주기점이 발생한다. 틀:수학 변수번째의 분기점 틀:수학 변수를 틀:수학로 나타낸다고 한다. 이때, 틀:수학에서 틀:수학는 다음과 같은 값으로 수렴하는 것으로 알려져 있다.틀:Sfn

더욱이 틀:수학 변수의 감소의 비율의 극한은 다음 식에서 보이는 상수 값으로 되는 것이 알려져 있다.틀:Sfn

이 틀:수학 변수의 값은 수리물리학자인 미첼 파이겐바움에 의해 발견된 것으로 파이겐바움 상수라고 불린다.틀:Sfn 틀:수학는 파이겐바움점이라고 불린다.틀:Sfn 주기배가 캐스케이드의 과정에서는 틀:수학 변수과 틀:수학은 적당한 크기 변환에 의해 국소적으로 완전히 일치하는 성질을 가진다.틀:Sfnm 이 자기유사성을 이용한 재규격화라고 불리는 수법에 의해 파이겐바움 상수는 구할 수 있다.틀:Sfnm 이상과 같은 로지스틱 사상이 주기배가 캐스케이드의 과정에서 보이는 성질은 후술과 같이 더욱 넓은 모임 (집합론)의 사상에서도 보편적으로 나타난다.틀:Sfn

어느 매개변수에 대해 궤도가 안정되는 최종적인 움직임을 한눈에 보기 위해서는 근사적인 분기 다이어그램인 궤도 다이어그램이 유용하다.틀:Sfnm 이 다이어그램에서는 분기 다이어그램과 같이 가로축으로 매개변수 틀:수학 변수를 취하고, 세로축으로 변수 틀:수학 변수를 취한다.틀:Sfnm 컴퓨터 등을 사용하고, 매개변수를 정하며, 예를 들면 500회 반복 계산을 행한다.틀:Sfn 그리고 계산 결과의 처음 100회를 무시하고 남은 400회의 결과만을 다이어그램에 표시한다.틀:Sfn 이에 따라 초기의 과도한 움직임은 무시 가능하고, 궤도의 점근적인 거동이 남는다.틀:Sfn 예를 들면 어느 틀:수학 변수에 대해 한 점이 표시됐을 때 이는 고정점이고, 어느 틀:수학 변수에 대해 틀:수학 변수점이 표시됐을 때 이는 틀:수학 변수주기 궤도에 상당한다.틀:Sfn 로지스틱 사상에 대해 궤도 다이어그램을 그리면 안정적인 주기 궤도를 나타내는 가지가 분열해가는 모습을 볼 수 있고, 이것이 주기배가 분기의 캐스케이드를 나타낸다.틀:Sfn

매개변수 a₁ = 3부터 a_∞ = 3.56994…의 사이에서 일어나는 주기배가 분기 캐스케이드의 궤도 다이어그램. 64주기(a₅) 이후는 간격이 매우 좁게 되고, 거의 보이지 않게 된다.

매개변수가 주기배가 캐스케이드의 집적점 틀:수학일 때, 변수 틀:수학은 영원히 닫히지 않는 비주기 궤도로 끌어당겨진다.틀:Sfn 바꿔 말하면 틀:수학에서는 무한 주기의 주기점이 존재한다.틀:Sfn 이 비주기 궤도는 파이겐바움 끌개(Feigenbaum attractor)틀:Sfnm나 임계 2^∞ 끌개(Critical 2^∞ attractor)틀:Sfnm라고 불린다. 끌개란 주위의 궤도를 끌어당기는 성질을 가진 영역을 가리키는 용어로, 끌어들여져 최종적으로 계속되는 궤도를 말한다.틀:Sfnm 여태까지 서술해 온 흡인적인 고정점이나 주기점도 끌개와 비슷하다.틀:Sfn

파이겐바움 끌개의 구조는 칸토어 집합이라는 프랙탈 도형과 같은 구조로 되어있다.틀:Sfnm 파이겐바움 끌개를 구성하는 점은 무한 개이며 게다가 그 농도는 실수와 동일하다.틀:Sfn 한편, 구성하는 점의 어느 두 점을 골라도 그 사이에 불안정한 주기점이 반드시 존재하고, 점의 분포는 연속적이지는 않다.틀:Sfn 또, 파이겐바움 끌개의 프랙탈 차원은 하우스도르프 차원 혹은 용량 차원으로 대강 0.54임이 알려져 있다.틀:Sfnm

칸토어 집합의 구성 예시. 선분의 한가운데 3분의 1을 무한히 계속 제거하면 길이는 0으로 아무 것도 남지 않는 것처럼 보여 점의 수는 비가산 무한으로 각각의 점의 아주 작은 근방 안에도 다른 점들이 무한히 포함되는 도형이 만들어진다.틀:Sfn

3.56994… < a < 4의 경우

혼돈의 출현

매개변수 틀:수학 변수가 틀:수학를 넘으면 로지스틱 사상은 혼돈이라고 불리는 움직임을 보인다.틀:Sfn 혼돈이란 대략적으로 말하면, 로지스틱 사상을 나타내는 차분 방정식처럼 확률적인 모호함이 없고 다음의 상태가 완전히 유일하게 결정됨에도 불구하고 발생하는 복잡하고 불규칙한 움직임을 말한다.틀:Sfn 로지스틱 사상의 틀:수학의 범위는 혼돈 영역(Chaotic region)이라고 불린다.틀:Sfnm

혼돈이 가지는 본질의 한 가지가 나비 효과라는 말로 상징되는 예측 불가능성이다.틀:Sfn 이는 혼돈에 의해 초기의 상태의 미세한 차이가 뒤의 상태에 거대한 차이를 가져오는 성질에 기인한다.틀:Sfn 이산 역학계에서 말하면 2개의 초기 조건 틀:수학과 틀:수학이 아무리 가까운 값이라 해도 시간 틀:수학 변수이 어느 정도 진행되면, 각각의 목적지 틀:수학 변수와 틀:수학은 현저히 떨어져버린다.틀:Sfn 예를 들면 틀:수학를 사용하고, 틀:수학과 틀:수학이라는 극히 가까운 2개의 초기 조건으로 각각의 궤도를 계산하면, 그 차는 반복 29회를 넘었을 때부터 그림에서는 확실히 알 정도로 거시적인 차이로 성장한다.틀:Sfn

이상과 같은 초기 조건의 민감성(initial condition sensitivity)라 불리는 혼돈의 성질은 랴푸노프 지수(Lyapunov exponent)에 의해 정량적으로 나타난다. 1차원 사상의 경우, 랴푸노프 지수 틀:수학 변수는 다음과 같이 계산 가능하다.틀:Sfn

여기서 틀:수학는 자연로그를 의미한다. 이 틀:수학 변수는 2개의 궤도의 거리（틀:수학 변수과 틀:수학의 거리)가 지수 함수적으로 어느 정도의 속도로 멀어지는가를 의미하는 지표로, 틀:수학 변수의 값이 양수라면 초기 조건 민감성을 가진 계임을 의미하고, 0 또는 음수라면 초기 조건 민감성이 없는 것임을 의미한다.틀:Sfn 실제로 로지스틱 사상의 틀:수학 변수를 수치적으로 계산하면 틀:수학의 범위에서는 틀:수학 변수는 0 또는 음의 범위로 머물며, 틀:수학의 범위에서 틀:수학 변수가 양수를 취하게 되는 것을 확인할 수 있다.틀:Sfn

창, 간헐성

매개변수가 틀:수학을 넘어서도 움직임의 매개변수 틀:수학 변수 로의 의존의 방법은 단순하지 않다.틀:Sfn 틀:수학 의 혼돈 영역에서는 많은 정교한 수학적 구조가 숨어 있다.틀:Sfn 이 영역에서는 계속 혼돈이 이어지는 것은 아니고, 안정적인 주기 궤도도 다시 나타난다.틀:Sfn 틀:수학에서의 움직임은 크게 나누면 이하의 두 종류로 나눠진다.틀:Sfn

• 안정적인 주기점. 이 경우, 랴푸노프 지수는 음수를 보인다.
• 비주기적 궤도. 이 경우, 랴푸노프 지수는 정수를 보인다.

틀:수학의 안에 존재하는 안정적인 주기점의 영역은 주기창(periodic window) 혹은 단순히 창(window)이라고 불린다.틀:Sfnm 혼돈 영역을 궤도 다이어그램으로 보면 비주기적 궤도의 영역은 무수히 많은 점으로 이루어져있고, 이에 둘러싸여 흩어져있는 공백 부분이 창이다.틀:Sfn

a = 3.55에서 a = 4까지의 로지스틱 사상의 궤도 다이어그램(그림 안에서는 매개변수가 r 표기)

각 창에서는 틀:수학보다 앞에서 일어난 주기배가 분기의 캐스케이드가 다시 일어난다.틀:Sfn 단, 이들의 주기는 전과 같은 틀:수학의 안정적인 주기 궤도가 아닌, 틀:수학나 틀:수학와 같은 새로운 안정적인 주기 궤도가 생성된다.틀:Sfn 처음은 틀:수학 변수주기에서 주기배가 캐스케이드가 일어나는 창은 주기 틀:수학 변수의 창 등으로 불린다.틀:Sfn 예를 들면 주기 3의 창은 틀:수학 부근의 영역에 존재하고 있고, 이 영역 안에서는 틀:수학라는 식으로 주기가 배가해간다.틀:Sfn

a = 3.8285에서 일어난 과도적 혼돈의 모양. 3주기 궤도에 흡인되기까지 혼돈적인 움직임을 보인다.

창의 영역에서는 혼돈은 사라져 존재하지 않고, 배후에 존재한다.틀:Sfn 그러나 이 혼돈은 불안정하기에 안정적인 주기 궤도만이 관측된다.틀:Sfn 창의 영역에서는 궤도가 초기 조건에서 안정적인 주기 궤도로 흡인되기까지 이 잠재적인 혼돈이 나타난다.틀:Sfn 이와 같은 혼돈을 과도적 혼돈(Transient chaos)이라고 부른다.틀:Sfn 이와 같이 혼돈이 잠재적으로 존재하고 있는 점에 있어서 창은 틀:수학보다 전에 나타난 주기 궤도와는 다르다.틀:Sfn

창의 수는 틀:수학의 범위에 무한 개 있다.틀:Sfn 각각의 창의 주기는 다양하고, 틀:수학 이상의 모든 자연수에 대응하는 주기의 창이 존재한다.틀:Sfn 그러나 각 주기의 창이 각각 1회씩 발생하는 것은 아니다.틀:Sfn 틀:수학 변수의 값이 클수록 그 주기의 창은 많이 반복해서 발생한다.틀:Sfn 주기 3의 창은 1회분으로, 예를 들면 주기 13의 창은 315회 발생한다.틀:Sfn 그 주기 3의 창에서 3주기 궤도가 생기면 샤르코우스키 순서가 완성되고, 모든 주기의 궤도가 출현한다.

틀:수학 변수가 소수일 경우로 한정하면 주기 틀:수학 변수의 창의 개수는

라는 식으로 계산할 수 있다.틀:Sfn 이 식은 틀:수학 변수를 소수로 한정해 도출되는 것이나, 실제로 소수가 아닌 틀:수학 변수의 안정적인 틀:수학 변수주기점의 수에 대해서도 좋은 정밀도로 계산할 수 있다.틀:Sfn

창의 폭(창이 시작되는 틀:수학 변수와 창이 끝나는 틀:수학 변수의 차)는 주기 3의 창이 가장 넓고, 주기가 클수록 폭은 좁아진다.틀:Sfn 예를 들면 주기 13의 창의 폭은 틀:수학 정도이다.틀:Sfn 어림에 따르면 닫힌구간 틀:Closed-closed의 안의 대강 틀:수학가 창의 영역으로, 남은 것이 혼돈 궤도가 지배하는 영역으로 되어있다.틀:Sfnm

틀:수학 변수를 늘려갈 때에 일어나는 혼돈에서 창으로의 변화는 접선의 분기라고 불리는 분기에 의해 일어난다.틀:Sfn 이는 사상의 곡선이 틀:수학의 대각선에 분기의 순간에 접하고, 더욱이 매개변수를 변화시키면 곡선과 직선이 접해 두 개의 고정점을 가지게 되는 분기이다.틀:Sfn 주기 틀:수학 변수의 창이면 반복 사상 틀:수학가 접선의 분기를 일으키는 것에 의해 안정적인 틀:수학 변수주기 궤도가 생겨난다.틀:Sfn 주기 3의 창의 접선의 분기에 대해서는 정확한 분기점의 값이 알려져 있고, 이 분기점 틀:수학 변수의 값을 틀:수학으로 하면 틀:수학이다.틀:Sfn 이 분기의 개요는 틀:수학의 그래프(세로축 틀:수학·가로축 틀:수학 변수의 그래프)를 고찰하는 것으로 이해할 수 있다.틀:Sfn

이 분기점 틀:수학보다 아주 살짝 작은 틀:수학일 경우의 틀:수학의 움직임을 보면 불규칙 변화에 더해 거의 세 주기로 주기적 변화하는 움직임도 존재하며, 이들이 교대로 발생하는 모양이 확인된다.틀:Sfn 이러한 주기적 움직임 부분은 층류(Laminar)라고 불리며, 불규칙적 움직임 부분은 파열(Burst)라고 불린다.틀:Sfnm 파열과 층류의 시간대의 길이에 규칙성은 없고, 불규칙하게 변화한다.틀:Sfn 그러나, 이보다도 틀:수학에 가까운 틀:수학이라는 값에서 움직임을 관찰하면 틀:수학의 경우보다 층류의 평균적인 시간 길이가 길게 되고, 파열의 평균적인 시간 길이가 짧게 된다.틀:Sfn 더욱이 틀:수학 변수를 크게 하면 층류의 길이가 점점 커지고, 틀:수학에 이르렀을 때에 완전한 3주기로 바뀐다.틀:Sfn

이와 같이 층류라는 질서적인 운동과 파열이라는 혼란스러운 운동이 간헐적으로 반복해 일어나는 현상은 간헐성(intermittency)이나 간헐적 혼돈(intermittent chaos)이라고 불린다.틀:Sfnm 매개변수 틀:수학 변수를 반대로 틀:수학에서 작게 하는 방향으로 생각해보면, 이는 혼돈의 발생의 일종으로 된다.틀:Sfn 매개변수가 창에서 멀어지는 방향으로 움직일 수록 파열이 지배적으로 되고, 최종적으로는 완전한 혼돈 상태로 된다.틀:Sfn 이도 전술한 주기배가 분기와 같이 혼돈에 이르는 일반적인 루트의 하나로, 이러한 접선의 분기에 의한 간헐적 혼돈의 발생을 특징으로 한 루트는 간헐적 루트(intermittency route)라고 불린다.틀:Sfnm

f ³(x)의 그래프에서 나타나는 채널의 모양

간헐성의 발생 매커니즘 또한 사상의 그래프에서 이해할 수 있다.틀:Sfn 틀:수학 변수가 틀:수학보다 매우 살짝 작은 경우, 틀:수학의 그래프와 대각선의 사이에서는 매우 작은 간격이 존재한다.틀:Sfn 이 간격은 채널 혹은 통로(channel)라고 불리며, 좁은 채널을 궤도가 통과하기 위해 많은 사상의 반복이 일어난다.틀:Sfn 이 채널을 통과하는 과정에서는 틀:수학과 틀:수학은 매우 가까운 값으로 되고, 실질적으로 거의 3주기 궤도와 같이 변수가 변화한다.틀:Sfn 이것이 층계에 상당한다.틀:Sfnm 궤도는 이윽고 이 좁은 채널을 빠져나오지만, 사상의 광역적인 구조의 결과, 다시 채널로 돌아온다.틀:Sfnm 채널과 멀어지는 사이는 혼돈적인 흐트러진 움직임을 한다.틀:Sfnm 이것이 파열에 상당한다.틀:Sfnm

띠, 창의 끝

혼돈 영역의 전체로 눈을 옮기면, 혼돈이어도 창이어도 궤도 다이어그램의 세로축의 최댓값과 최솟값(끌개의 상한치와 하한치)은 어느 범위 내로 한정돼있다.틀:Sfn 식 (틀:EquationNote)이 보이듯 로지스틱 사상의 최댓값은 틀:수학로 주어지고, 이것이 끌개의 상한치로 된다.틀:Sfn 끌개의 하한치는 틀:수학의 점 틀:수학로 주어진다.틀:Sfn 결국, 궤도 다이어그램에서 틀:수학 변수가 움직이는 최댓값과 최솟값은 매개변수 틀:수학 변수에 의존해

으로 주어진다.틀:Sfn 최종적으로는 틀:수학로 궤도는 닫힌구간 틀:Closed-closed 전체에 미친다.틀:Sfn

궤도 다이어그램을 관찰하면 점의 분포에 특징적인 밀도가 보인다.틀:Sfn 점이 짙은 부분은 변수가 그 주변의 값을 취하는 빈도가 크다는 것을 의미하고, 점이 옅은 부분은 변수가 그 주변의 값을 취하는 빈도가 작다는 것을 의미한다.틀:Sfn 이러한 점의 빈도의 차이는 로지스틱 사상의 그래프의 형태에 기인해 생겨난다.틀:Sfn 그래프의 맨 꼭대기 틀:수학 부근이 높은 빈도로 궤도를 끌어들이고, 그곳에서 대응된 곳인 틀:수학 부근도 높은 빈도로 되며, 그곳에서 대응된 곳인 틀:수학 부근도 높은 빈도로 되고… 라는 식으로 빈도의 분포가 생겨난다.틀:Sfn 사상에 의해 생겨난 점의 밀도 분포는 불변 측도(invariant measure)나 분포 함수라고 불리는 양으로 특징지어지며, 끌개의 불변 측도는 초기 조건에 관계 없이 재현성이 있다.틀:Sfnm

궤도 다이어그램 혼돈 영역의 초기 부근, 틀:수학 변수가 처음 2주기배가 캐스케이드의 집적점 틀:수학를 조금 넘은 부근을 보면 궤도가 몇 개의 구간으로 나뉘어져 있는 것이 관찰된다.틀:Sfn 이와 같이 나뉘어진 작은 영역은 띠(band)라고 불린다.틀:Sfn 띠가 복수인 경우, 궤도는 규칙적으로 순번으로 각 띠를 돌며, 게다가 각 띠 내에서 취하는 값은 불규칙적으로 되는 움직임을 보인다.틀:Sfn 이러한 혼돈 궤도는 띠 혼돈(band chaos)나 주기적 혼돈(periodic chaos)라고 불리며, 틀:수학 변수개의 띠에서 생기는 혼돈은 틀:수학 변수띠 혼돈 등으로 불린다.틀:Sfnm 2띠 혼돈이면, 대강 틀:수학의 범위 내에 존재하고 있다.틀:Sfn

띠 구조의 모양. e_p의 간격이 급격히 작아지기에 8띠 이상은 표시돼있지 않다. 궤도를 포함하는 최상단과 최하단의 선이 식 (틀:EquationNote)의 범위 내에 있다.

2띠 혼돈의 좌단 틀:수학에서 더욱이 값을 작게 하면, 주기배가 분기의 경우와 같이 띠의 수가 2배씩 증가한다.틀:Sfn 틀:수학띠 혼돈이 분열해 틀:수학띠 혼돈으로 되는 분기점 혹은 틀:수학 변수띠 혼돈이 융합해 틀:수학띠 혼돈으로 되는 분기점을 틀:수학 변수(단 틀:수학)로 나타낸다고 한다. 그러면 주기배가 분기와 같이 틀:수학에서 틀:수학 변수는 어느 값에 집적한다.틀:Sfnm 이 집적점 틀:수학에서 띠의 수는 무한으로 되고, 틀:수학의 값은 틀:수학의 값과 일치한다.틀:Sfnm

로지스틱 사상의 궤도 다이어그램 전체의 자기유사 층계 구조

틀:수학보다 전에 나타난 주기배가 캐스케이드의 분기점에 대해서도 비슷하게 틀:수학 변수안정 주기 궤도가 분기해 틀:수학안정 주기 궤도로 되는 분기점을 틀:수학 변수(단 틀:수학)로 나타낸다고 한다. 이때, 틀:수학부터 틀:수학까지의 궤도 다이어그램에 주목하면 틀:수학부터 틀:수학까지의 전체 궤도 다이어그램의 축소판이 틀:수학부터 틀:수학까지의 궤도 다이어그램의 안에 두 개 존재한다.틀:Sfn 비슷하게 틀:수학부터 틀:Math까지의 궤도 ㅏ이어그램에 주목하면 틀:수학부터 틀:수학까지의 전체 궤도 다이어그램의 축소판이 틀:수학부터 틀:수학까지의 궤도 다이어그램의 안에 네 개 존재한다.틀:Sfn 이하도 같게 틀:수학 변수부터 틀:수학 변수까지의 궤도 다이어그램에는 전체 궤도 다이어그램의 축소판이 틀:수학 변수개 존재하며, 로지스틱 사상의 분기 구조는 무한한 자기유사 층계를 갖추고 있다.틀:Sfn

로지스틱 사상의 창의 자기유사 층계 구조

분기 구조의 자기유사 층계는 창의 안에서도 존재한다.틀:Sfn 창의 안의 주기배가 캐스케이드는 틀:수학주기 분기의 캐스케이드와 같은 루트를 탄다.틀:Sfn 결국, 창의 안에서 무한 번의 주기배가 분기가 일어나고, 이를 통과하면 움직임은 다시 혼돈으로 된다.틀:Sfn 예를 들면 주기 3의 창에서는 틀:수학에서 안정적인 주기 궤도의 캐스케이드가 끝난다.틀:Sfn 틀:수학를 통과하면 움직임은 3의 배수의 띠 혼돈으로 된다.틀:Sfn 틀:수학 변수가 틀:수학에서 증가함에 따라 이 띠 혼돈도 2개씩 융합하고, 창이 끝나는 마지막에는 띠의 수는 세 개로 된다.틀:Sfn 이러한 창의 안에 있는 띠의 안에서도 무수히 많은 창이 또 더욱이 존재한다.틀:Sfnm 결국, 창의 안에서는 틀:수학의 궤도 다이어그램 전체의 축소판이 포함돼있는 형태로 되고, 창의 안에서도 분기의 자기유사 층계 구조가 존재한다.틀:Sfnm

창이 끝나면 광범위의 혼돈으로 돌아온다. 주기 3의 창이면 틀:수학에서 마지막 3띠 혼돈이 큰 범위의 1띠 혼돈으로 변해 창이 끝난다.틀:Sfnm 그러나 이 변화는 비연속적으로, 3띠의 혼돈 끌개는 돌연 크기를 변화시키고, 1띠로 변한다.틀:Sfn 이와 같이 끌개의 크기가 비연속적으로 변하는 현상은 고비현상(crisis)라고 불린다.틀:Sfn 창이 끝나 일어나는 종류의 고비현상은 특히 내부고비현상(interior crisis)라고도 불린다.틀:Sfnm 창이 끝나 고비현상이 일어날 때, 안정적인 주기 궤도가 궤도 다이어그램에서는 보이지 않는 불안정 주기점과 접촉한다.틀:Sfn 이에 따라 주기 궤도가 빠져나올 수 있는 출구가 생기고, 내부고비현상이 발생한다.틀:Sfn 내부고비현상 직후에는 어느 시간대에서는 광역 혼돈으로 움직이나, 또 어느 시간대에서는 본래의 띠 혼돈적 움직임도 일으키고, 창의 시작과 같은 일종의 간헐성이 나타난다.틀:Sfn

a = 4의 경우

매개변수 a = 4의 로지스틱 사상의 거미줄 그림(왼쪽)과 n = 500까지의 시계열 그림(오른쪽). 초기 조건 x₀ = 0.3의 경우.

매개변수가 틀:수학에 이르면 움직임은 닫힌구간 틀:Closed-closed 전역을 돌아다니는 혼돈으로 된다.틀:Sfn 이때, 랴푸노프 지수 틀:수학 변수는 최대로 되고, 가장 혼돈이 강한 상태라고 할 수 있다.틀:Sfn 틀:수학의 로지스틱 사상의 틀:수학 변수는 정확한 값을 구할 수 있고, 그 값은 틀:수학다.틀:Sfn 혼돈의 엄밀한 수학적 정의는 아직 통일돼있지 않으나, 잘 알려져 있는 혼돈의 정의의 하나에 대해 틀:수학의 로지스틱 사상은 닫힌구간 틀:Closed-closed 위에서 혼돈적틀:Efn임이 증명 가능하다.틀:Sfnm

a = 4일 경우의 불변 측도 ρ (x)의 그래프. 점（높이를 ρ (x)로 맞춤)은 10000회 반복으로 얻은 실제 점의 빈도를 보인다.

점의 밀도는 불변 측도 틀:수학도 틀:수학의 경우는 다음과 같은 정확한 함수로 얻을 수 있다.틀:Sfn

여기서 틀:수학는 사상을 반복했을 때의 점 틀:수학 변수의 모든 점 수에 대해 점 틀:수학 변수이 미소 구간 틀:Closed-closed에 들어가는 점의 수의 비율이 틀:수학로 주어진다는 의미를 가진다.틀:Sfn 틀:수학의 로지스틱 사상의 빈도 분포는 닫힌구간 틀:Closed-closed의 양쪽 사이드 부근에서 밀도가 높고, 틀:수학에서 가장 밀도가 낮은 형태를 하고 있다.

틀:수학의 경우, 혼돈 궤도와는 달리 모든 주기의 주기 궤도도 존재한다.틀:Sfn 자연수 틀:수학 변수에 대해 틀:수학의 그래프는 틀:수학개의 극대와 틀:수학개의 극소가 존재하는 곡선으로 되고, 게다가 이 모든 극대와 극소는 틀:수학과 틀:수학에 접하는 상태로 된다.틀:Sfn 따라서 대각선과 그래프의 교점의 수는 틀:수학개 있고, 틀:수학의 고정점은 틀:수학개 존재한다.틀:Sfn 이 틀:수학개의 고정점에는 틀:수학 변수주기점도 반드시 포함되므로 틀:수학에서는 임의의 틀:수학 변수주기 궤도가 존재한다.틀:Sfn 이와 같이 틀:수학의 경우 닫힌구간 틀:Closed-closed 위에서는 주기점이 무한히 존재하나, 이들 주기점은 모두 불안정하다.틀:Sfn 또, 닫힌구간 틀:Closed-closed이라는 비가산 무한의 집합에 대해 이들 주기점의 수는 가산 무한이고, 거의 모든 초기 조건에서 시작되는 궤도는 주기 궤도로는 되지 않고 비주기 궤도로 된다.틀:Sfn

로지스틱 사상 f_a=4의 궤도를 0과 1의 기호열로 변환하면 모든 기호열이 재현 가능하다.

혼돈의 중요성의 하나로 결정론적 성질과 확률론적 성질의 이중성이 있다.틀:Sfn 역학계는 결정론적인 과정이지만, 변수가 취하는 범위를 적당히 조망화(coarse graining)하면 확률적인 과정과 구별이 가능하게 된다.틀:Sfn 틀:수학의 로지스틱 사상의 경우면 모든 동전 던지기의 결과를 로지스틱 사상의 궤도로 기술 가능하다.틀:Sfn 이를 상술하면 다음과 같다.틀:Sfnm

틀:수학의 확률로 앞뒤가 나오는 동전 던지기를 가정하고, 몇 번이고 동전 던지기를 계속한다. 앞면이 나올 때를 틀:수학, 뒷면이 나올 때를 틀:수학이라 하면 앞, 뒤, 앞, 앞, 뒤hellip;라는 결과는 틀:수학과 같이 기호열로 된다. 한편, 로지스틱 사상의 궤도 틀:수학에 대해서 틀:수학 이하의 것은 틀:수학으로, 틀:수학을 넘는 것은 틀:수학로 변환해 궤도를 틀:수학과 틀:수학에서 생기는 기호열로 치환한다. 예를 들어 초기 조건 틀:수학으로 하면 틀:수학로 되므로 궤도는 틀:수학이라는 기호열로 된다. 전자의 동전 던지기에 의한 기호열을 틀:수학 변수라 하고, 후자의 로지스틱 사상에 의한 기호열을 틀:수학 변수로 한다. 기호열 틀:수학 변수에서는 랜덤한 동전 던지기에서 기호를 정한 것으로 모든 패턴의 수열이 생겨날 수 있다. 따라서 로지스틱 사상에 의한 기호열 틀:수학 변수이 어떤 것이라 해도 틀:수학 변수의 안에 동일한 것이 존재한다. 그리고 이 역이 성립한다. 즉, 어떠한 틀:수학 변수의 기호열이어도, 초기 조건을 적절히 고르기만 하면 로지스틱 사상의 궤도 틀:수학 변수에 의해 실현 가능하다. 즉, 임의의 틀:수학 변수에 대해 틀:수학로 되는 틀:수학이 닫힌구간 틀:Closed-closed 안에 그저 한 점 존재한다.틀:Sfnm

a > 4의 경우

a = 4.5의 로지스틱 사상에서는 닫힌구간 [0, 1]의 거의 모든 점에서 출발하는 궤도는 마이너스 무한대로 향한다.

매개변수 틀:수학 변수가 틀:수학를 넘으면 로지스틱 사상의 그래프의 꼭짓점 틀:수학는 틀:수학을 넘는다.틀:Sfn 그래프가 틀:수학을 돌파한 범위에서 궤도는 닫힌구간 틀:Closed-closed을 바져나오게 된다.틀:Sfn 그 결과, 닫힌구간 틀:Closed-closed의 거의 모든 점에서 출발하는 궤도는 어느 시점에서 닫힌구간 틀:Closed-closed을 빠져나오고, 최종적으로 마이너스 무한대로 발산한다.틀:Sfn

이 틀:수학에서 일어나는 분기도 고비현상의 일종으로, 특히 경계 고비현상 혹은 경계 분기점(boundary crisis)이라고 불린다.틀:Sfn 이 경우의 경계 고비현상에서는 닫힌구간 틀:Closed-closed에 있던 끌개가 불안정화·붕괴하고, 게다가 바깥쪽에 끌개도 존재하지 않기에 궤도가 무한히 멀리 발산한다.틀:Sfn

한편, 틀:수학의 조건 하에서도 닫힌구간 틀:Closed-closed의 안에 계속 머무르는 궤도가 있다.틀:Sfnm 알기 쉬운 예시는 닫힌구간 틀:Closed-closed 안의 고정점이나 주기점으로, 이들은 닫힌구간 틀:Closed-closed의 안에서 계속 머무른다.틀:Sfnm 그러나 닫힌구간 틀:Closed-closed의 안에서 계속 머무르는 궤도에는 고정점이나 주기점 이외의 궤도도 존재한다.틀:Sfn

틀:수학을 만족하는 틀:수학 변수의 구간을 틀:수학으로 한다. 위와 같이 변수 틀:수학 변수이 틀:수학으로 일단 들어가면 마이너스 무한대로 발산한다. 사상을 1회 적용하면 틀:수학으로 대응하는 틀:수학 변수도 닫힌구간 틀:Closed-closed의 안에 존재한다. 이 틀:수학 변수의 구간은 두 개로 나뉘고 이들을 묶어서 틀:수학로 한다. 비슷하게 사상을 1회 적용하면 틀:수학으로 대응하는 구간도 네 개 존재하고, 이들을 틀:수학로 한다. 이하도 같게 틀:수학 변수회 반복으로 틀:수학에 이르는 구간 틀:수학 변수이 틀:수학개 존재한다.틀:Sfn 따라서 다음과 같이 닫힌구간 틀:Closed-closed에서 틀:수학 변수을 무한 번 제거한 구간 틀:수학 변수가 틀:수학 변수의 안에 계속 머무르는 궤도의 모임이다.틀:Sfn

닫힌구간 틀:Closed-closed에서 틀:수학 변수을 제거하는 작업은 상술한 칸토어 집합의 구성 과정과 비슷하고, 실제로 틀:수학 변수는 칸토어 집합(닫힌 완전 분리로 닫힌구간 틀:Closed-closed의 완전 부분집합)의 형태로 닫힌구간 틀:Closed-closed의 안에 존재한다.틀:Sfnm 그리고 더욱이 틀:수학 변수 위에 로지스틱 사상 틀:수학는 혼돈적이다.틀:Sfn

a < 0의 경우

로지스틱 사상은 생태학 상의 모델로 연구된 경위도 있고, 매개변수 틀:수학 변수가 음수일 경우에 대해 논의된 수는 적다. 틀:수학 변수를 틀:수학부터 감소시키면 틀:수학에서는 틀:수학의 안정적인 고정점에 점근하지만, 틀:수학을 넘은 때부터 2주기점으로 분기하고, 양수일 때와 같이 주기배가 분기를 거쳐 혼돈에 이른다. 최종적으로는 틀:수학를 밑돌고 플러스 무한대로 발산하게 된다.

매개변수 a가 −2부터 4까지의 궤도 다이어그램. 음수 쪽도 양수 쪽도 이들의 매개변수 범위를 넘으면 발산한다.

특별한 경우의 엄밀해

매개변수 틀:수학 변수가 특정 로지스틱 사상에 대해서는 시각 틀:수학 변수과 초기 조건 틀:수학을 양으로 포함하는 엄밀해가 이하와 같이 얻을 수 있다.

틀:수학의 경우

틀:수학의 경우

틀:수학의 경우

이상 세 개의 엄밀해를 고찰하면 어느 해도 틀:NumBlk 라는 형태로 된다. 여기서 틀:수학 변수는 어떤 적절한 함수, 틀:수학은 그 역함수를 의미한다. 틀:수학에서는 틀:수학, 틀:수학에서는 틀:수학, 틀:수학에서는 틀:수학이다. 단, 임의의 틀:수학 변수에 대해서 일반적으로 로지스틱 사상의 엄밀해를 나타내는 것이 가능한 수학적으로 표준적인 함수의 틀:수학 변수는 존재하지 않는다.

보편성

같은 종류의 움직임을 보이는 사상의 모임

사인 함수 (틀:EquationNote)의 그래프

사인 함수 (틀:EquationNote)의 궤도 다이어그램

로지스틱 사상에서 나타난 위와 같은 분기의 패턴은 로지스틱 사상에 한정되지 않는다.틀:Sfn 어느 조건을 만족한 사상에서 이 분기 패턴이 공통해서 나타난다.틀:Sfn 다음의 사인 함수를 사용한 역학계는 그 일례이다.틀:Sfn

여기서 정의역은 틀:수학 동시에 틀:수학으로 한다.틀:Sfn 이 사인 함수 (틀:EquationNote)은 로지스틱 사상 (틀:EquationNote)와 정성적으로 동일한 움직임을 일으킨다.틀:Sfn 즉, 이 사상에서도 로지스틱 사상과 같이 매개변수 틀:수학 변수의 증가와 함께 주기배가 루트를 거쳐 혼돈으로 되고, 더욱이 혼돈 영역에서는 창이 비슷하게 존재한다.틀:Sfn

로지스틱 사상도 사인 함수도 닫힌구간 틀:Closed-closed을 닫힌구간 틀:Closed-closed에 대응하는 1차원 사상으로, 단봉(unimodal)이라고 불리는 다음의 성질을 만족한다.틀:Sfn

1. 틀:수학을 만족한다.
2. 사상은 미분가능하고, 닫힌구간 틀:Closed-closed 안에 틀:수학을 만족하는 임계점 틀:수학 변수가 하나 존재한다.

일반적으로 한 매개변수·한 변수가 있는 1차원 사상이 단봉으로 꼭짓점 부근을 2차의 다항식으로 근사한 곡선이면, 구체적인 사상의 형태에 의존하지 않고, 매개변수 범위 틀:수학에서 본 무한의 주기배가 캐스케이드의 분기가 일어나고, 더욱이 식 (틀:EquationNote)에서 정의된 비율 틀:수학 변수는 파이겐바움 상수 틀:수학에 일치한다.틀:Sfnm

또, 로지스틱 사상에서 나타난 안정 주기 궤도의 출현 패턴에도 보편성이 있다.틀:Sfn 매개변수를 틀:수학 변수로 하고, 틀:수학에서 나타나는 단봉형 사상에서는 2개의 고정점과 불안정한 어느 매개변수 구간에서 다양한 주기의 안정 주기 궤도가 계속 출현하고, 그 출현 패턴(어느 주기의 안정 주기 궤도의 출현 횟수와 출현 순서)는 공통임이 알려져 있다.틀:Sfn 즉, 이 종류의 사상이면 사상의 구체적인 형태에 따르지 않고 안정 주기 궤도의 계열은 같게 된다.틀:Sfn 로지스틱 사상의 경우는 틀:수학가 그 매개변수 구간이었으나, 사인 함수 (틀:EquationNote)에서는 틀:수학이 공통하는 안정 주기 궤도의 계열이 일어나는 매개수 구간이다. 이 보편성이 있는 안정 주기 궤도의 계열은 U계열(U sequence)이라고 불린다.틀:Sfn

게다가 로지스틱 사상은 닫힌구간 틀:Closed-closed 위에서 슈바르치안이 항상 음수라는 성질을 가진다. 어느 （틀:수학급의） 사상 틀:수학 변수의 슈바르치안은

로 정의되는 함수이다.틀:Sfn 실제로 로지스틱 사상의 슈바르치안을 계산하면

으로 되고, 틀:수학 변수 및 틀:수학 변수의 값에 따르지 않고 슈바르치안은 음수로 된다.틀:Sfn 닫힌구간 틀:Closed-closed을 닫힌구간 틀:Closed-closed로 대응하는 1차원 사상이 단봉으로 음의 슈바르치안을 가지면 존재하는 안정 주기 궤도는 많아도 1개라는 성질이 알려져 있다.틀:Sfn

위상 공액인 사상

기호 틀:수학으로 사상의 합성을 나타낸다고 한다. 일반적으로 위상 공간 틀:수학에 대해 두 개의 사상 틀:수학와 틀:수학가 위상동형사상 틀:수학에 의해

라는 관계를 가질 때, 틀:수학 변수와 틀:수학 변수는 위상 공액(phase conjugation)라고 한다.틀:Sfn 위상 공액인 틀:수학 변수와 틀:수학 변수는 본질적으로 동일한 움직임을 보이고, 틀:수학 변수의 움직임이 주기적이면 틀:수학 변수도 주기적이며, 틀:수학 변수의 움직임이 혼돈적이면 틀:수학 변수도 혼돈적이다.틀:Sfn

특히 위상동형사상 틀:수학 변수가 선형이면 틀:수학 변수와 틀:수학 변수는 선형 공액(linearly conjugation)이라고 한다.틀:Sfn 모든 이차 함수는 다른 모든 이차 함수와 선형 공액이다.틀:Sfn 따라서 틀:NumBlk 틀:NumBlk 틀:NumBlk 등은 임의의 매개변수 틀:수학 변수의 로지스틱 사상과 선형 공액이다.틀:Sfnm 식 (틀:EquationNote)이나 식 (틀:EquationNote)의 형태도 로지스틱 사상이라고 불리기도 한다.틀:Sfnm 특히 식 (틀:EquationNote)의 형태라면 계산량이 줄기에 장시간을 필요로 하는 수치 계산에 편리하다.틀:Sfn

텐트 사상 (틀:EquationNote)의 궤도의 모양. a = 4의 로지스틱 사상과 위상 공액인 관계를 가진다.

또 틀:수학의 로지스틱 사상 틀:수학는 다음의 텐트 사상(tent map) 틀:수학나 베르누이 시프트 사상(Bernoulli shift map) 틀:수학과 위상 공액인 관계이다.틀:Sfn

로지스틱 사상 틀:수학가 엄밀히 혼돈적임의 증명이나, 틀:수학의 엄밀해 (틀:EquationNote)의 도출에 이들의 위상 공액의 관계를 이용할 수 있다.틀:Sfnm

혹은 기호역학계(symbolic dynamical systems)의 사고방식을 도입해 위에서 도입했듯 틀:수학과 틀:수학의 열에서 생기는 기호열 공간 상에서 정의되는 다음과 같은 시프트 사상 틀:수학 변수를 생각한다고 한다.틀:Sfn

여기서 틀:수학 변수는 틀:수학 또는 틀:수학이다. 식 (틀:EquationNote)에서 도입한 집합 틀:수학 변수 위에서 로지스틱 사상 틀:수학는 시프트 사상과 위상 공액이므로 이를 이용해 틀:수학 변수 위의 틀:수학가 혼돈적임을 이끌어낼 수 있다.틀:Sfn

생물 개체수 모델로의 로지스틱 사상

이산형 개체군 모델

로지스틱 사상은 영국의 수리생물학자 로버트 메이(Robert McCredie May)의 연구를 발단으로 생물의 개체수의 변화를 생각하는 식으로 세상에 널리 알려졌다.틀:Sfnm 이러한 생물 개체수로의 로지스틱 사상에서는 변수 틀:수학 변수은 어느 환경 안에서 서식하는 생물의 개체수(보다 전문적으로는 개체군 사이즈)를 의미한다.틀:Sfn 더욱이 개체가 그 환경에서 나오거나 외부의 개체가 환경으로 들어오거나 하지 않는 경우(혹은 이출입이 있어도 실질적인 영향이 없는 경우)를 가정하고, 이러한 상황에서의 개체수의 증감을 생각하는 수리 모델이 수리생물학 상의 로지스티컬 사상이다.틀:Sfn

생물의 개체수의 증식을 생각하는 수리 모델에는 차분 방정식을 사용한 이산적인 시간의 모델과 미분방정식을 사용한 연속적인 시간의 모델의 두 종류가 있다.틀:Sfn 예를 들면 알을 낳으면 바로 죽는 종류의 곤충으로는 그 곤충의 개체수는 1세대째의 개체수, 2세대째의 개체수…라는 식으로 각 세대마다로 셀 수 있다.틀:Sfn 이와 같은 예시는 전자의 이산 시간 모델로 적합하다.틀:Sfn 한편, 각 세대가 연속적으로 서로 겹치는 경우는 연속 시간 모델과 친화성이 있다.틀:Sfn 로지스틱 사상은 이러한 이산형 혹은 세대 분산형의 개체군 모델에 상당한다.틀:Sfnm

어느 환경 안의 단일종 생물의 개체수를 틀:수학 변수으로 나타낸다고 한다. 가장 단순한 개체수의 증식의 방법으로 개체수에 대해 항상 일정한 비율로 계속 증가하는 모델을 생각할 수 있다. 그러한 개체수 증가 모델은 맬서스 성장 모델이라고 불리며, 다음과 같은 형태로 나타난다.틀:Sfn

여기서 틀:수학 변수은 틀:수학 변수세대째의 개체수를 의미하고, 틀:수학 변수는 개체수의 증식률로 양의 정수이다.틀:Sfn 그러나 모델 (틀:EquationNote)에서는 개체수가 무진장으로 계속 늘어나며 대부분의 실현상에 대해 비현실적인 모델이라 할 수 있다.틀:Sfnm 어느 환경이 길러낼 수 있는 개체수에는 한도가 있으므로 개체수 틀:수학 변수이 증가하면 증식률 틀:수학 변수는 저하하는 것이 자연스럽다고 여겨진다.틀:Sfn 이와 같이 개체수 밀도의 변화에 따라 증식률이 변화하는 것을 밀도의존성이라고 부른다.틀:Sfn 밀도의존성을 모델 (틀:EquationNote)에 반영한 개량 모델로 가장 단순한 것으로 해 다음과 같은 차분 방정식이 생각된다.틀:Sfn

여기서 틀:수학 변수는 그 환경 안에서 가능한 최대증식률을 의미하고, 틀:수학 변수는 밀도의존성의 영향의 강도를 의미한다.틀:Sfn 모델 (틀:EquationNote)는 증식률이 개체수에 단순히 비례해 낮아지는 것으로 가정한다.틀:Sfn 식 (틀:EquationNote)의 틀:수학 변수을

으로 변수 변환하면 이하의 로지스틱 사상이 도출된다.틀:Sfn

생물의 개체수로 식 (틀:EquationNote) 혹은 식 (틀:EquationNote)를 다룰 때에는 틀:수학 변수 혹은 틀:수학 변수이 음수로 되면 개체수로의 의미를 하지 않게 된다.틀:Sfn 그렇게 되지 않기 위해 초기 조건 틀:수학에 대해 틀:수학이라는 조건이 매개변수 틀:수학 변수에 대해 틀:수학라는 조건이 요구된다.틀:Sfn

외에는 가정하고 있는 환경이 길러낼 수 있는 최대 개체수 틀:수학 변수를 가정하고, 이를 사용해

라는 형태로 밀도의존성을 이용한 차분 방정식을 생각하고, 틀:수학로 변수 변환해 로지스틱 사상을 이끌어내는 것도 있다.틀:Sfn 이 경우, 변수 틀:수학 변수은 최대 개체수 틀:수학 변수에 대한 개체수 틀:수학 변수의 비율을 의미한다.틀:Sfn

로지스틱 방정식의 이산화

로지스틱 사상은 연속 시간형의 개체군 모델인 로지스틱 방정식의 이산화로부터도 도출 가능하다.틀:Sfn 로지스틱 사상의 이름도 로버트 메이가 로지스틱 방정식의 이산화에서 로지스틱 사상을 도입한 것에서 유래한다.틀:Sfn 로지스틱 방정식이란 다음과 같은 생물 개체수의 시간 변화를 나타내는 상미분 방정식이다.틀:Sfn

여기서 틀:수학 변수은 생물 개체수나 개체수 밀도, 틀:수학 변수는 연속적인 시간, 틀:수학 변수와 틀:수학 변수가 매개변수이다. 틀:수학 변수는 환경용량, 틀:수학 변수는 생물 번식 능력이라고도 불리고, 보통은 양수를 취한다.틀:Sfn 이 식의 좌변 틀:수학은 시각 틀:수학 변수의 개체군 사이즈의 변화 속도를 의미한다.틀:Sfn

로지스틱 방정식의 해의 예시. 개체수 N은 시간 t가 경과하면 초기 조건에 따르지 않고 환경용량 K로 수렴한다.

로지스틱 방정식 (틀:EquationNote)은 로지스틱 사상 (틀:EquationNote)와 비슷해보이나, 해의 움직임은 로지스틱 사상과는 크게 다르다.틀:Sfn 초기 조건 틀:수학이 양수인 한, 로지스틱 방정식의 개체수 틀:수학 변수은 항상 단조롭게 틀:수학 변수로 수렴할 뿐이다.틀:Sfn

이 로지스틱 방정식에 1계 상미분 방정식의 수치 해석적 방법의 하나인 오일러 방법에 의한 차분화 근사를 실행하는 것에 따라 로지스틱 사상을 도출 가능하다.틀:Efn 오일러 방법의 차분화 근사란 적당한 시간 간격 틀:수학 변수를 도입하고, 증식률 틀:수학을 이하와 같이 근사하는 것이다.틀:Sfnm

이 근사의 결과, 다음의 로지스틱 사상을 이끌어낼 수 있다.틀:Sfnm

단, 이 식의 틀:수학 변수과 틀:수학 변수는 전의 매개변수, 변수, 시간 간격으로 다음과 같은 관계를 가진다.틀:Sfnm

틀:수학 변수가 충분히 작다면 식 (틀:EquationNote)은 전의 식 (틀:EquationNote)의 유효한 근사로 작동하고, 틀:수학에서는 전의 식의 해와 일치한다.틀:Sfn 한편, 틀:수학 변수가 크면 전의 식의 해에서 벗어난다.틀:Sfn 또, 식 (틀:EquationNote)의 관계에서 틀:수학 변수를 크게 하는 것은 매개변수 틀:수학 변수를 크게 하는 것에 상당한다.틀:Sfn 따라서, 틀:수학 변수를 크게 할 수록, 전의 방정식과의 오차를 단순히 크게하는 것 뿐만 아니라 해에 혼돈적 움직임을 만들어내는 것으로 된다.틀:Sfn

자리매김

위와 같이, 생물의 개체군 동태론 상에서는 로지스틱 사상은 이산형 증식 과정의 모델의 하나이다. 단, 생물의 개체수의 모델로의 로지스틱 사상은 물리학의 법칙 등과는 달리, 직접적인 실험 결과나 보편적으로 성립하는 원리에서 이끌어내진 것은 아니다.틀:Sfn 도출 과정의 사고방식에 어느 정도의 합리성은 있으나, 기본적으로는 머릿속에서 생각된 '모델'에 그친다.틀:Sfn 로지스틱 사상을 저명하게 한 메이 또한, 논하고 있는 모델이 개체수의 증감을 정확히 표현하고 있다고 주장하고 있는 것은 아니다. 생물 개체군 역학계의 연구 상에서도 역사적으로 다용돼온 것은 미분 방정식에 의한 연속 시간 모델이고, 이들 연속 시간 모델의 적용에 따라 생물 개체군 역학계의 이해를 깊이 해왔다.틀:Sfn 밀도의존성을 고려한 이산 시간 개체군 모델로도 개체수가 음수로 되지 않는 리커 모델(Ricker model) 쪽이 더욱 현실적이라 할 수 있다.틀:Sfn

일반적으로 말할 수 있는 것으로, 수리 모델은 개체군 역학계에 관한 중요한 정성적 정보를 제공해주는 것도 있지만, 실험적인 뒷받침이 없다면 수리 모델에서 나오는 결과를 너무 진지하게 받아들이면 안 된다.틀:Sfn 수리 모델의 결론이 생물학적 연구 결과로부터 벗어나는 경우가 있어도, 더욱이 수리 모델에 의한 연구가 의미가 있는 것은 유용한 대조로 될 수 있기 때문이다.틀:Sfn 모델의 구성 과정이나 설정 혹은 모델이 전제로 한 생물학적 식견이나 가설을 재점검하는 것에 따라 생물학적 논점을 제시할 수 있는 가능성이 있다.틀:Sfn 생물 개체수 모델로의 로지스틱 사상은 너무 단순해 현실적이지는 않으나, 로지스틱 사상이 보이는 결과는 환경으로부터의 불규칙적인 영향 등에 무관계하게 개체군 그 자체에 내재하는 역학계에 의해 개체수의 다양한 변동이 일어날 수 있는 가능성을 암시한다.

응용

결합 사상계

1 변수의 로지스틱 사상은 계로의 자유도 혹은 차원은 틀:수학이다.틀:Sfnm 한편 실제 자연계에서는 시간적으로 흐트러질 뿐만 아니라 다수의 공간 자유도를 가지고 공간적으로도 흐트러지는 다자유도의 혼돈이 많다고 추정된다.틀:Sfn 혹은 혼돈적 운동을 행하는 진동자의 동기화 현상도 연구 대상이다.틀:Sfn 이러한 것을 조사하기 위해 차분 방정식(사상)을 여러 번 결합시킨 결합 사상(coupled map)의 수법이 있다.틀:Sfn 결합 사상 모델 연구의 제재로 로지스틱 사상이 종종 채용된다.틀:Sfnm 그 이유로는 로지스틱 사상 자체는 이미 혼돈의 전형적 모델로 잘 알려져 있고, 그 조사의 축적이 있음을 들 수 있다.틀:Sfn

결함 사상 모델에서의 구체적인 결합의 방법으로는 다양한 수법이 존재한다.틀:Sfn 전부 틀:수학 변수개의 사상이 결합하고, 틀:수학 사상번째의 사상의 시각 틀:수학 변수의 상태가 틀:수학로 나타낸다고 한다. 대국적 결합 사상(globally coupled map)이라고 불리는 수법에서는 틀:수학를 다음과 같이 정식화한다.틀:Sfnm

결합 진동자의 연구의 흐름에서는 다음과 같이 변수의 차분에서 진동자 두 개 틀:수학 변수와 틀:수학 변수를 결합시킨 가장 간단한 다음의 모델 등을 들 수 있다.틀:Sfn

이들의 식 안의 틀:수학가 결합 사상 모델에 집어넣는 구체적인 사상이고, 로지스틱 사상이 사용되는 경우는 여기에서 적용된다.틀:Sfnm

a = 3.8과 D = 0.43의 결합 사상 모델 (틀:EquationNote)의 두 개의 변수의 변화（위쪽）과 이들의 차（아래쪽）. 두 개의 변수는 동기화 후에 갑자기 비동기화 상태로 되고, 다시 동기화 상태로 돌아온다.

식 (틀:EquationNote) 및 (틀:EquationNote) 안의 틀:수학 변수이나 틀:수학 변수는 결합 계수(coupling coefficient) 등으로 불리는 사상끼리의 결합의 세기를 의미하는 매개변수이다.틀:Sfnm 한편, 로지스틱 사상을 결합 사상 모델에 집어넣는 경우, 로지스틱 사상의 매개변수 틀:수학 변수는 모델의 비선형성의 세기를 의미한다.틀:Sfn 틀:수학 변수의 값과 틀:수학 변수 또는 틀:수학 변수의 값을 변화시키는 것으로 로지스틱 사상의 결합 사상계에서는 다양한 현상이 나타난다. 예를 들면 모델 (틀:EquationNote)에서는 틀:수학 변수를 어떤 값 틀:수학 이상으로 크게 하면 틀:수학 변수와 틀:수학 변수는 동기화하면서 혼돈 진동을 일으킨다.틀:Sfn 틀:수학 미만에서도 항상 제각기 다른 혼돈 진동이 일어날 뿐만이 아니다.틀:Sfn 틀:수학 변수가 있는 범위일 때는 틀:수학임에도 불구하고 틀:수학 변수와 틀:수학 변수는 2주기 진동을 일으킨다.틀:Sfn 틀:수학에서는 동기화 상태와 비동기화 상태가 교대로 계속 일어나는 움직임도 보인다.틀:Sfn

대자유도의 대국적 결합 사상 (틀:EquationNote)에 로지스틱 사상을 적용한 연구에서는 혼돈적 순회 혹은 혼돈적 편력(chaotic itinerancy)이라고 불리는 현상도 발견됐다.틀:Sfnm 이는 몇 개의 군집(cluster)으로 모여 진동하는 질서적인 상태에서 흐트러진 상태로 되고, 다시 다른 군집 상태로 되고, 또다시 흐트러진 상태로 되고…라는 움직임을 반복하는 현상으로, 위상 공간 상에서 끌개의 잔해(the remains of an attractor)라고 불리는 영역을 궤도가 돌아다니는 것에서 일어난다고 추정된다.틀:Sfnm

유사난수 생성기

컴퓨터 시뮬레이션이나 정보 보안 분야에서는 계산기로 유사난수를 작성하는 것이 중요한 기술의 하나로, 유사난수를 만드는 수법의 하나로 혼돈의 활용이 생각된다. 혼돈으로부터의 유사난수 생성기로 충분한 성질을 가진 것은 아직 실현되지 않았으나, 여태 몇 가지의 수법이 제안돼왔다. 로지스틱 사상에 대해서도 여태 혼돈에 기반한 유사난수 생성기의 가능성이 여러 연구자들에 의해 연구돼왔다.

로지스틱 사상의 유사난수 생성에는 매개변수 틀:수학가 잘 이용되고 있다. 역사적으로도 후술과 같이 전자 계산기의 탄생으로부터 곧 1947년에 스타니스와프 울람과 존 폰 노이만도 틀:수학의 로지스틱 사상을 사용한 유사난수 생성기의 가능성을 지적했다. 그러나 로지스틱 사상 틀:수학의 점의 분포는 식 (틀:EquationNote)에서 나타나는 분포로 돼있고, 나오는 수치가 틀:수학과 틀:수학 가까이로 치우친다. 이로 인해 치우치지 않는 균일난수를 얻기 위해서는 어떠한 처리를 필요로 한다. 그 방법으로는

1. 얻은 수치를 텐트 사상 (틀:EquationNote)과의 관계를 이용해 균일분포로 변환하는 방법
2. 얻은 수치를 상술한 동전 던지기의 비유와 같이 역치(threshold)를 사용해 틀:수학이나 틀:수학로 변환하고, 이를 반복해서 균일난수의 비트열을 얻는 방법

등이 있다. 또, 로지스틱 사상에서 얻은 수열의 틀:수학과 틀:수학은 강한 상관 관계를 지니고 있고, 유사난수의 수열로는 문제가 있다. 이를 해소하는 방법 중 하나는 사상 1회 적용마다의 수열 틀:수학를 만드는 것이 아닌 적당한 틀:수학회 반복마다 수열 틀:수학를 만들 필요가 있다. 예를 들면 가장 좋은 방법에 대해서는 틀:수학 또는 틀:수학이고, 두 번째로 좋은 방법은 틀:수학으로 양호한 유사난수를 얻을 수 있다고 여겨진다.

컴퓨터를 사용해 디지털로 혼돈을 계산하는 일반적 문제로 컴퓨터에서는 유한 계산 정밀도로 계산하기 때문에 혼돈 본래의 진정으로 비주기적인 수열을 원리적으로 얻을 수 없고, 대신 유한 주기열이 출력된다는 문제점이 있다. 원리적으로 비주기열을 얻을 수 없는 경우여도 유사난수 생성을 위해서는 가능한 한 긴 주기의 수열이 바람직하다. 그러나 단정밀도 부동소수점 수(single-precision floating-point) 계산에서 로지스틱 사상 틀:수학가 실제로 출력하는 수열의 주기성을 조사한 결과에 따르면 할당된 비트수에서 가능한 최대 주기에 비해 실제로 출력되는 수열의 주기는 매우 작게 되는 것이 보고됐고, 이 관점에서 메르센 트위스터와 같은 기존의 유사난수 생성기에 비해 로지스틱 사상에 의한 유사난수 생성은 뒤떨어진다고 지적됐다. 또, 로지스틱 사상 틀:수학에서는 계산 도중에 수치가 고정점 틀:수학으로 떨어지고, 그대로 일정하게 유지될 위험도 있다. 한편, 로지스틱 사상에서는 열린구간 틀:Open-open의 안에서 항상 값을 취하므로 부동소수점 뿐만 아니라 고정소수점에서도 문제 없이 계산 가능하고, 고정소수점 계산의 이점을 누릴 수 있다. 고정소수점이면 같은 비트수로 비교해 부동소수점보다 긴 주기의 수열로 되는 것이나 의도하지 않은 틀:수학으로의 수렴이 없어진다는 것이 지적되고 있다.

복소수로의 확장

로지스틱 사상의 궤도 다이어그램(위쪽)과 망델브로 집합（아래쪽）의 대응 관계

이는 복소 해석함수로 정의된 역학계도 흥미를 가질 수 있는 대상으로,틀:Sfn 그 예시가 다음의 이차 함수에서 정의되는 역학계이다.틀:Sfnm

단, 여기서의 매개변수 틀:수학 변수와 변수 틀:수학 변수는 복소수이다.틀:Sfnm 이 사상은 로지스틱 사상 (틀:EquationNote)와 기본적으로는 같은 것이라 할 수 있다.틀:Sfn 위에서도 서술했듯, 사상 (틀:EquationNote)은 선형 함수에 의해 로지스틱 사상 (틀:EquationNote)와 위상 공액인 관계이다.틀:Sfnm

매개변수 틀:수학 변수를 고정하고, 초기 조건 틀:수학을 바꾸면서 사상 (틀:EquationNote)의 반복의 이후를 계산할 때, 틀:수학에서도 틀:수학 변수이 무한대로 발산하지 않는 틀:수학의 집합을 충만한 쥘리아 집합(filled Julia set)이라고 한다.틀:Sfn 더욱이 충만한 쥘리아 집합의 경계를 쥘리아 집합이라고 한다.틀:Sfn 또, 초기 조건을 틀:수학으로 고정하고, 매개변수 틀:수학 변수를 바꾸면서 사상 (틀:EquationNote)의 반복을 계산했을 때, 틀:수학 변수가 무한대로 발산하지 않는 틀:수학 변수의 집합을 망델브로 집합이라고 한다.틀:Sfn 사상 (틀:EquationNote)의 쥘리아 집합이나 망델브로 집합으로부터 프랙탈 도형이 생성된다.틀:Sfnm

특히 망델브로 집합에서는 도형의 각 원반은 어떠한 주기의 점근적 안정인 주기 궤도의 영역에 상당한다.틀:Sfn 로지스틱 사상의 궤도 다이어그램과 망델브로 집합의 도형을 나란히 하면 로지스틱 사상 궤도 다이어그램의 점근적 안정인 고정점, 주기배가 분기, 주기 3의 창 등이 망델브로 집합 도형과 실수축 위에서 대응하고 있음을 알 수 있다.틀:Sfnm

시간 지연을 가진 경우

지연 로지스틱 사상의 궤도의 모습. 좌우의 그림에서 초기 조건 (x₀, y₀)은 같으나, a = 2에서의 분기를 경계로 궤도가 끌어당겨진 곳이 닫힌 곡선（왼쪽）과 점（오른쪽）으로 나뉘어져있다.

로지스틱 사상을 생물의 각 세대의 개체수를 나타내는 모델로 해석하면 다음 세대의 개체수가 현재 세대의 개체수 뿐만 아니라 그 하나 이전 세대의 개체수도 현재 세대에 영향을 주는 경우도 생각된다.틀:Sfn 그러한 예시가

라는 차분 방정식으로, 하나 이전 세대의 개체수 틀:수학이 마이너스의 밀도의존성으로 식에 들어가있다.틀:Sfn 틀:수학으로 두면 식 (틀:EquationNote)는 다음과 같은 2 변수 차분 방정식으로 치환할 수 있다.틀:Sfn

이 역학계는 준주기 끌개(quasi-periodic attractor)의 분기의 연구 등에서 이용되고, 지연 로지스틱 사상(delayed logistic map)이라고 불린다.틀:Sfn 지연 로지스틱 사상에서는 틀:수학에서 네이마르크-색커 분기(Neimark-Sacker bifurcation)(Neimark는 Ju. I. Neimark이고, Sacker는 R. Sacker이다)가 일어나고, 점근적 안정적인 고정점이 불안정하게 되며, 그 불안정한 고정점의 주변에 점근적 안정적인 불변 곡선이 생긴다.틀:Sfn

연구사

혼돈 명명 이전

사상의 반복이 동역학계와 관련한 의미를 가지기 이전의 시대에는 수학자 가스통 쥘리아와 피에르 파투(Pierre Fatou)가 복소함수의 반복에 대해서 연구했다. 쥘리아와 파투의 연구는 해석 함수를 중심으로 한 광범위한 것이었는데틀:Sfn 특히 식 (틀:EquationNote)에서도 보인 이하의 복소 이차 함수의 움직임이 1920년대에 그들에 의해 연구됐다.틀:Sfn

쥘리아와 파투도 쥘리아 집합의 안에 혼돈적 움직임을 이해하고 있었으나, 당시는 컴퓨터 그래픽 등도 없었기에 그들을 잇는 인물이 나타나지 않고, 연구는 그치게 되었다.틀:Sfn 이후 1970년대 후반까지 복소 역학계(complex dynamics) 연구는 계속해서 시들했고, 복소평면 위의 사상의 역학계적 움직임이 주목되는 것은 브누아 망델브로 등의 등장을 기다리게 된다.틀:Sfn

스타니스와프 울람

존 폰 노이만

1947년, 수학자 스타니스와프 울람과 존 폰 노이만은 “On combination of stochastic and deterministic processes”（확률론적 과정과 결정론적 과정의 결합에 관해）라는 짧은 보고서에서

라는 이차 함수의 반복 합성으로 유사난수를 생성할 수 있다는 것을 지적했다.틀:Sfn 이 식은 현재의 시점으로는 틀:수학의 로지스틱 사상에 상당한다.틀:Sfn 당시 '혼돈'이라는 말도 아직 사용돼지 않았으나, 울람과 폰 노이만은 비선형 함수에 의한 복잡한 수열의 생성에 이미 주목했던 것이라고 할 수 있다. 또, 울람과 폰 노이만의 보고서에서는 사상 (틀:EquationNote)와 텐트 사상이 위상 공액의 관계에 있는 것이나, 이 사상의 수열의 불변 측도가 식 (틀:EquationNote) 에서 주어지는 것도 밝혔다.틀:Sfn

이후 임의의 매개변수 틀:수학 변수를 갖춘 형식의 이차 사상에 대해서도 상세한 조사가 몇 가지 있었다. 1958년부터 1963년에 걸쳐 핀란드의 수학자 페카 뮈르버그(Pekka Myrberg)는 틀:수학 변수를 매개변수로 하는

라는 형식의 이차 사상의 분기 현상을 조사했다. 이 일련의 연구는 역학계로서 본질적인 것으로, 뮈르버그는 이 사상의 주기배가 분기 캐스케이드를 조사해 집적점 틀:수학의 존재도 보였다. 외에는 1964년 소련의 올렉산드르 샤르코우스키(Oleksandr Mykolayovych Sharkovsky), 1969년 프랑스의 이고르 구모브스키(Igor Gumowski)와 크리스찬 미라(Christian Mira), 1973년의 니콜라스 메트로폴리스(Nicholas Constantine Metropolis) 등의 작업이 로지스틱 사상과 같은 단순한 1 변수 차분 방정식의 이상한 움직임을 밝혀냈다.틀:Sfn

로버트 메이의 연구

로버트 메이(2009년 촬영)

이후 1970년 초반에 수리생물학자 로버트 메이(Robert McCredie May)가 생태학의 문제에 몰두하는 과정에서 식 (틀:EquationNote)의 모델을 알게 된다.틀:Sfn 메이는 로지스틱 방정식의 이산 시간화부터 식 (틀:EquationNote) 즉 로지스틱 사상을 도입했다.틀:Sfn 로지스틱 사상의 움직임을 수리적으로 해석했고, 메이는 1973년과 1974년에 그 성과를 발표했다.틀:Sfn 로지스틱 사상의 수치 실험이 행해졌고, 매개변수 틀:수학 변수에 의한 움직임의 변화가 조사됐다.틀:Sfn 1976년에는 ”Simple mathematical models with very complicated dynamics”(극히 복잡한 움직임을 지니는 단순한 수리 모델)이라는 논문을 네이처에서 발표했다.틀:Sfn

1976년의 논문은 고찰 논문으로, 로지스틱 사상을 제재로 하면서 단순한 비선형 함수에서도 주기배가 분기 캐스케이드나 혼돈과 같은 복잡한 움직임이 일어나는 것에 대해 강조했고, 주의를 재촉하는 내용이었다.틀:Sfnm 특히 이 논문은 메이의 수리생물학자로의 지위, 연구 결과의 명쾌함, 그리고 무엇보다 단순한 포물선의 식이 복잡한 움직임을 만들어낸다는 충격적인 내용으로 큰 반향을 일으켜 과학계에 받아들여졌다.틀:Sfn 이러한 메이의 연구를 거쳐 로지스틱 사상은 많은 연구자를 혼돈 연구로 이끌었고, 혼돈 연구의 흐름을 새로이 재시작시켰다고 평가될 정도로 저명한 수리 모델로 되었다.틀:Sfnm

메이의 연구 이후

메이는 리톈옌(Tien-Yien Li)과 J. A. 요크(J. A. Yorke)가 논문 ”Period three implies chaos”(3주기는 혼돈을 의미한다)에서 사용한 '혼돈'이라는 표현을 적극적으로 사용했고, 이 논문도 주목됐다. 이론도 있으나, 이 리와 요크의 논문은 '혼돈'이라는 말을 수학 용어로 처음 사용했다고 추정되며, 해당 논문에 의해 결정론적인 무질서적 움직임을 가리키는 용어 '혼돈'이 생겨났다고 여겨진다.틀:Sfnm 리와 요크는 1973년에 해당 논문을 일단 완성시켰으나, 더 아메리칸 매스매티컬 먼슬리(The American Mathematical Monthly)에 투고한 결과 연구 색이 너무 강하므로 알기 쉽게 대폭 다시 쓰라는 통보를 받고 게재가 기각됐다.틀:Sfn 이후 논문은 수정되지 않고 내버려져 있었다. 그러나 이듬해 1974년에 리와 요크가 있던 메릴랜드 대학교에 메이가 특별 초대 강의로 찾아와 로지스틱 사상의 이야기를 했다. 당시 메이는 로지스틱 사상의 혼돈 영역에서 무엇이 일어나는지 아직 이해를 하지 못했으나, 리와 요크 또한 로지스틱 사상의 주기배가 캐스케이드에 대해서 알지 못했다.틀:Sfn 메이의 이야기에 흥분한 리와 요크는 강의 후 메이를 붙잡아 둘이서 얻어낸 결과의 이야기를 했다.틀:Sfn 바로 리와 요크는 기각된 논문을 다시 썼고, 재제출된 논문은 1975년에 출판됐다.틀:Sfn

미첼 파이겐바움(2006년 촬영)

또 1975년 즈음, 수리생물학자 미첼 파이겐바움은 로지스틱 사상의 주기배가 캐스케이드에 주목했고, 분기값이 등비수열적으로 수렴하는 척도 법칙을 알게 됐고, 오늘날 파이겐바움 상수라고 불리는 상수의 존재를 수치 실험에서 발견했다.틀:Sfn 메이도 조지 오스터(George Frederick Oster)와 함께 그 척도 법칙을 알게 됐으나, 깊이 들어가지는 못했다.틀:Sfn 파이겐바움은 식 (틀:EquationNote)에서 보인 사인 함수에서도 같은 상수가 나타나는 것을 발견했고, 이 척도 법칙에는 로지스틱 사상만으로 그치지 않는 보편성이 있다는 것을 알게 됐다.틀:Sfn 1980년에는 이 결과에 대한 엄밀한 증명이 P. 콜렛(Pierre Collet), J-P. 에크맨(Jean-Pierre Eckmann), 오스카 랜포드(Oscar Lanford) 등에 의해 나오게 됐다.틀:Sfnm 파이겐바움과 거의 동시기 혹은 그 뒤, 물리학자들에 의해 실제 현상에 같은 주기배가 캐스케이드와 파이겐바움 상수가 발견됐고, 어디까지나 수학적 현상으로 간주됐던 혼돈은 물리학 방면에서도 큰 충격을 주었다.틀:Sfnm

단 혼돈 유행 이전의 연구 성과가 경시됐고, 그들의 연구 성과의 대부분이 로지스틱 사상 등을 이용한 재발견자의 공적 취급을 받는 풍조에 대한 비판도 있다. 메이 자신도 선행 연구가 있었다는 것을 존중한 뒤 자신의 공적은 '이차 사상의 기괴한 수학적 거동을 독립적으로 최초로 발견'이라고 한 것이 아닌 자신은 '마지막으로 과학의 그 광범위한 의미를 강조한 연구자들' 중 한 명이라고 자리매김했다.틀:Sfn 수학자 로버트 L. 드바니(Robert L. Devaney)는 저서에서 로지스틱 사상의 해설에 들어가기 전에 다음과 같이 말했다.틀:Sfn 틀:인용문 틀:인용문

같이 보기

• 로지스틱 함수
• 랴푸노프 안정성

참고 문헌

• 틀:저널 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용

• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:저널 인용

외부 링크

• 틀:매스월드
• 틀:매스월드
• 틀:매스월드
• 틀:매스월드