베르누이 수

틀:위키데이터 속성 추적 수론에서, 베르누이 수(Bernoulli數, 틀:Llang)는 거듭제곱수의 합이나 탄젠트의 멱급수 전개 따위의 다양한 공식에 등장하는 유리수 수열이다. 야코프 베르누이와 세키 다카카즈가 비슷한 시기에 독립적으로 발견하였다.

정의

베르누이 수열 $B_n$은 다음과 같은 생성함수로 정의할 수 있다.

$\frac{t}{\exp (t)-1}=\sum _{n=0}^{\mathrm{\infty }}\frac{B_n{t}^n}{n!}$

보다 일반적으로, 다음이 성립한다.

$\frac{t{e}^{xt}}{e^t-1}=\sum _n\frac{t^n}{n!}\sum _{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})B_{n-k}{x}^k$

따라서, 베르누이 수열 $B_0,B_1,B_2,\dots$은 다음과 같다.

1, −1/2, 1/6, 0, −1/30, 0, 1/42, 0, −1/30, …

여기서 분자는 틀:OEIS이며, 분모는 틀:OEIS이다.

일부 저자들은 첫 베르누이 수를 $-1/2$ 대신 $+1/2$로 사용하기도 한다. 여기서는 이를 $\tilde{B}$로 표기하자.

${\tilde{B}}_i=(-1{)}^i{B}_i=\{\begin{array}{cc}+1/2& i=1\\ B_n& i\ne 1\end{array}$

$\frac{t}{1-\exp (-t)}=\sum _{n=0}^{\mathrm{\infty }}\frac{{\tilde{B}}_n{t}^n}{n!}$

베르누이 다항식

베르누이 다항식. 점차 사인 또는 코사인에 수렴하는 것을 알 수 있다.

베르누이 수 $B_n$가 주어졌을 때, 이로부터 다음과 같은 베르누이 다항식(틀:Llang) $B_n(x)\in \mathbb{Q}[x]$을 정의할 수 있다.

$B_n(x)=\sum _{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})B_{n-k}{x}^k$

이는 아펠 다항식열을 이룬다.

그렇다면, 베르누이 수는 베르누이 다항식으로부터 다음과 같이 얻을 수 있다.

$B_n=B_n(0)$

${\tilde{B}}_n=B_n(1)$

성질

$B_1=-1/2$을 제외하고, 홀수차 베르누이 수는 모두 0이다. 4의 배수차 베르누이 수는 음수이며, 4의 배수가 아닌 짝수차 베르누이 수는 양수이다.

$\mathrm{sgn}{B}_n=\{\begin{array}{cc}-1& n=1\\ 0& 1\ne n\equiv 1,3(\mathrm{mod}4)\\ -1& n\equiv 0(\mathrm{mod}4)\\ +1& n\equiv 2(\mathrm{mod}4)\end{array}$

생성 함수

베르누이 다항식의 생성 함수는 다음과 같다.

$\sum _{n=0}^{\mathrm{\infty }}{B}_n(x)\frac{t^n}{n!}=\frac{t\exp (xt)}{\exp (t)-1}$

따라서, 베르누이 수의 생성 함수는 다음과 같다.

$\sum _{n=0}^{\mathrm{\infty }}{B}_n\frac{t^n}{n!}=\frac{t}{\exp t-1}$

$\sum _{n=0}^{\mathrm{\infty }}{\tilde{B}}_n\frac{t^n}{n!}=\frac{t\exp t}{\exp t-1}$

대칭

베르누이 다항식은 다음 항등식들을 만족시킨다.

$B_n(1-x)=(-1{)}^n{B}_n(x)n\ge 0$

$(-1{)}^n{B}_n(-x)=B_n(x)+n{x}^{n-1}$

삼각 함수의 멱급수

베르누이 수는 탄젠트 및 코탄젠트의 매클로린 급수에 등장한다.

$\tan x=\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n-1}{2}^{2n}(2^{2n}-1)B_{2n}{x}^{2n-1}}{(2n)!}(|x|<\pi /2)$

$\cot x=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n{2}^{2n}{B}_{2n}{x}^{2n-1}}{(2n)!}$

마찬가지로, 쌍곡 탄젠트의 매클로린 급수는 다음과 같다.

$\tanh x=\sum _{n=1}^{\mathrm{\infty }}\frac{2^{2n}(2^{2n}-1)B_{2n}}{(2n)!}{x}^{2n-1}(|x|<\pi /2)$

푸리에 급수

베르누이 다항식의 푸리에 급수는 다음과 같다.

$B_n(x)=-\frac{n!}{(2\pi i{)}^n}\sum _{k=0}\frac{e^{2\pi ikx}}{k^n}=-2n!\sum _{k=1}^{\mathrm{\infty }}\frac{\cos (2k\pi x-\frac{n\pi }{2})}{(2k\pi {)}^n}$

따라서, 베르누이 다항식은 다음과 같이 사인 또는 코사인으로 수렴하는 것을 알 수 있다.

$\frac{(2\pi {)}^n}{n!}{B}_n(x)=-2\cos (2\pi x-\frac{n\pi }{2})+O(2^{-n})$

제타 함수와의 관계

$-x\zeta (1-x)$의 그래프

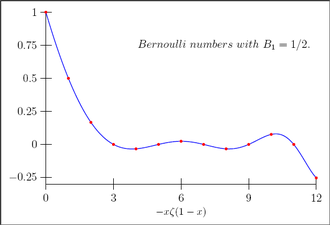
베르누이 수는 리만 제타 함수의 특수한 값이다.

${\tilde{B}}_n=(-{)}^n{B}_n=-n\zeta (1-n)=-\frac{2}{(2\pi {)}^n}\sin (\pi (1-n)/2)n!\zeta (n)$

따라서, 리만 제타 함수는 베르누이 수의 복소수 $n$에 대한 해석적 연속으로 볼 수 있다.

$n=0$일 경우 리만 제타 함수는 극을 갖지만, 이 경우 다음과 같이 극한을 취할 수 있다.

${\tilde{B}}_0=B_0=1=\underset{n\to 0}{\lim }-n\zeta (1-n)$

${\tilde{B}}_1=-B_1=-2\underset{n\to 1}{\lim }\frac{\sin (\pi (1-n)/2)}{(2\pi {)}^n}n!\zeta (n)=1/2$

따라서, 스털링 공식에 따라 짝수차 베르누이 수의 절댓값에 대하여 다음과 같은 점근 공식이 성립한다.

$|B_{2n}|=\frac{2(2n)!}{(2\pi {)}^{2n}}\zeta (2n)\sim 4\sqrt{\pi n}{\left(\frac{n}{\pi e}\right)}^{2n}(n\gg 1)$

보다 일반적으로, 베르누이 다항식은 후르비츠 제타 함수 $\zeta (s,q)$의 특수한 값이다.

$B_n(x)=-n\zeta (1-n,x)$

${\tilde{B}}_n=B_n(1)=-n\zeta (1-n,1)=-n\zeta (1-n)$

따라서, 후르비츠 제타 함수는 베르누이 다항식의 복소수 $n$에 대한 해석적 연속으로 볼 수 있다.

스털링 수와의 관계

베르누이 다항식과 베르누이 수는 제2종 스털링 수와 하강 포흐하머 기호로 다음과 같이 나타낼 수 있다.

$B_{n+1}(x)=B_{n+1}+\sum _{k=0}^n\frac{n+1}{k+1}\left\{\genfrac{}{}{0ex}{}{n}{k}\right\}{x}^{\underset{\_}{k+1}}$

$B_n=\sum _{k=0}^k(-1{)}^k\frac{k!}{k+1}\left\{\genfrac{}{}{0ex}{}{n}{k}\right\}$

이 경우 $B_1=-1/2$이 된다.

반대로, 하강 포흐하머 기호를 베르누이 다항식으로 다음과 같이 나타낼 수 있다.

$x^{\underset{\_}{n+1}}=\sum _{k=0}^n\frac{n+1}{k+1}\left[\genfrac{}{}{0ex}{}{n}{k}\right](B_{k+1}(x)-B_{k+1})$

여기서 $[\genfrac{}{}{0ex}{}{n}{k}]$는 제1종 스털링 수이다.

거듭제곱수의 합

임의의 자연수 $m$과 $n$에 대하여, 처음 $n$개의 $m$제곱수들의 합은 다음과 같다.

$\sum _{k=1}^n{k}^m=\frac{1}{m+1}\sum _{k=0}^m(-1{)}^k(\genfrac{}{}{0ex}{}{m+1}{k})B_k{n}^{m+1-k}=\frac{1}{m+1}(B_{m+1}(n+1)-B_{m+1}(0))$

이를 베르누이 공식(Bernoulli公式, 틀:Llang) 또는 파울하버 공식(틀:Llang)이라고 한다. 예를 들어, $m=1$일 경우, 1부터 $n$까지의 자연수의 합인 삼각수 공식을 얻을 수 있다.

$1+2+3+\cdots +n=\frac{1}{2}(B_0{n}^2-2B_1{n}^1)=\frac{1}{2}(n^2+n)$

$m=2,3$일 경우, 제곱수·세제곱수의 합 공식을 얻을 수 있다.

$1^2+2^2+3^2+\cdots +n^2=\frac{1}{3}(B_0{n}^3-3B_1{n}^2+3B_2{n}^1)=\frac{1}{3}(n^3+\frac{3}{2}{n}^2+\frac{1}{2}n)$

$1^3+2^3+3^3+\cdots +n^3=\frac{1}{4}(B_0{n}^4-4B_1{n}^3+6B_2{n}^2-4B_3{n}^1)=\frac{1}{4}(n^4+2n^3+n^2)$

베르누이 공식은 음계산법을 통하여 간단하게 적을 수 있다. 우선, 음변수 $𝖻$에 대하여 다음과 같은 선형 범함수를 정의하자.

$L:{𝖻}^n\mapsto B_n$

그렇다면

$L:(a+𝖻{)}^n\mapsto B_n(a)$

가 된다. 따라서,

$\sum _{k=1}^n{k}^m=\frac{1}{m+1}L((n+1+𝖻{)}^{m+1}-{𝖻}^{m+1})=L\underset{𝖻}{\overset{𝖻+n+1}{\int }}{x}^{m}dx$

이다.

알고리즘

베르누이 수를 계산하는 효율적인 알고리즘들이 알려져 있으며, $B_n$를 계산하는 가장 빠른 알려진 알고리즘의 시간 복잡도는

$O(n^2{\log }^{2+ϵ}n)$

이다.

수론적 성질

폰 슈타우트-클라우젠 정리(틀:Llang)에 따르면, 모든 양의 정수 $n$에 대하여, 만약 $B_n\ne 0$이라면 다음이 성립한다.

$B_n+\sum _{(p-1)\mid n}\frac{1}{p}\in \mathbb{Z}$

여기서 $\sum _{(p-1)\mid n}$은 $p-1$이 $n$의 약수가 되는 모든 소수 $p$에 대한 합이다. 즉, $B_n\ne 0$의 분모는 $\prod _{(p-1)\mid n}p$이다.

소수 $p$에 대하여 다음 두 조건이 서로 동치이며, 이를 만족시키는 소수를 정규 소수이라고 한다.

• $p\nmid B_{2n}\mathrm{\forall }2n\in \{2,4,6,\dots ,p-3\}$
• $p\nmid h_{\mathbb{Q}({\zeta }_p))}$. 여기서 $h_K$는 $K$의 유수이며, $\mathbb{Q}({\zeta }_p)$는 원분체이다.

이를 정규 소수의 쿠머 조건(틀:Llang)이라고 한다.

표

낮은 차수의 베르누이 수는 다음과 같다. 틀:OEIS, 틀:OEIS

n	Bn
0	1
1	−1/2
2	1/6
4	−1/30
6	1/42
8	−1/30
10	5/66
12	−691/2730
14	7/6
16	−3617/510
18	43867/798

낮은 차수의 베르누이 다항식은 다음과 같다.

$B_0(x)=1$

$B_1(x)=x-\frac{1}{2}$

$B_2(x)=x^2-x+\frac{1}{6}$

$B_3(x)=x^3-\frac{3}{2}{x}^2+\frac{1}{2}x$

$B_4(x)=x^4-2x^3+x^2-\frac{1}{30}$

$B_5(x)=x^5-\frac{5}{2}{x}^4+\frac{5}{3}{x}^3-\frac{1}{6}x$

$B_6(x)=x^6-3x^5+\frac{5}{2}{x}^4-\frac{1}{2}{x}^2+\frac{1}{42}$

역사

세키의 《괄요산법》

베르누이의 《추측술》 97쪽 (현대적으로 재조판)

러브레이스의 베르누이 수 계산 프로그램. 이는 세계 최초의 컴퓨터 프로그램이다.

1631년에 요한 파울하버(틀:Llang, 1580~1635)는 거듭제곱수의 합을 계산하는 알고리즘을 출판하였다. 파울하버의 알고리즘은 효율적이지만, 파울하버는 이를 베르누이 수를 통하여 나타내지 않았다. 이에 대하여 도널드 커누스는 다음과 같이 적었다. 틀:인용문2

세키 다카카즈(1642~1708)는 1712년 사후에 출판된 《괄요산법》(틀:Llang틀:Lang)에 거듭제곱수의 합에 대한 일반 공식 및 베르누이 수를 제시하였다. 《괄요산법》에는 산가지로 표기된 파스칼 삼각형 밑에 다음과 같이 처음 12개의 베르누이 수가 수록돼 있다.

一級	全
二級	取㆓二分之一㆒爲㆑加
三級	取㆓六分之一㆒爲㆑加
四級	空
五級	取㆓三十分之一㆒爲㆑減
六級	空
七級	取㆓四十二分之一㆒爲㆑加
八級	空
九級	取㆓三十分之一㆒爲㆑減
十級	空
十一級	取㆓六十六分之五㆒爲㆑加
十二級	空

즉, 분수 $k/n$은 n틀:Langk로 표시돼 있고, 부호는 양수일 경우 틀:Lang, 음수일 경우 틀:Lang로 표시돼 있다. (㆑, ㆒, ㆓와 같은 부호는 간분의 가에리텐(틀:Llang)이다.)

세키와 거의 동시에, 야코프 베르누이는 1713년 사후에 출판된 저서 《추측술》(틀:Llang) 2부 3장 97쪽에 거듭제곱수의 합의 일반 공식을 제시하였지만, 증명하지 않았다. 이 책에서 베르누이는 다음과 같이 적었다. 틀:인용문2

1830년대에 레온하르트 오일러와 콜린 매클로린은 오일러-매클로린 공식을 발견하면서 베르누이 수를 재발견하였다. 아브라암 드무아브르와 레온하르트 오일러는 "베르누이 수"라는 표현을 최초로 사용하였다. 1834년에 카를 구스타프 야코프 야코비는 베르누이 공식을 엄밀하게 증명하였다.

에이다 러브레이스는 1843년에 찰스 배비지의 해석기관에 대한 책의 주석 G(틀:Llang)에 베르누이 수를 계산하는 알고리즘을 기술하였다. 이 주석 G는 세계 최초의 컴퓨터 프로그램으로 여겨진다.

폰 슈타우트-클라우젠 정리는 카를 게오르크 크리스티안 폰 슈타우트(틀:Llang)와 토마스 클라우젠(틀:Llang) 이 1840년에 독자적으로 발견하였다. 정규 소수의 쿠머 조건은 에른스트 쿠머가 1850년에 증명하였다.

같이 보기

• 벨 수
• 오일러 수
• 베르누이 다항식
• 멱급수
• 테일러 급수
• 급수 (수학)
• 계승 (수학)

참고 문헌

• 틀:저널 인용
• 틀:저널 인용
• 틀:저널 인용
• 틀:저널 인용
• 틀:저널 인용
• 틀:저널 인용
• 틀:저널 인용
• 틀:저널 인용

외부 링크

• 틀:Eom
• 틀:매스월드
• 틀:매스월드
• 틀:매스월드
• 틀:매스월드
• 틀:매스월드
• 틀:매스월드
• 틀:웹 인용
• 틀:수학노트
• 틀:수학노트
• 틀:수학노트
• 틀:Nlab
• 틀:웹 인용