모스 이론

틀:위키데이터 속성 추적 미분위상수학에서 모스 이론(Morse理論, 틀:Llang)은 다양체의 위상수학을 그 위에 정의된 매끄러운 함수로 분석하는 분야이다. 이 경우 함수의 임계점을 통해 콤팩트 매끄러운 다양체 $M$의 호몰로지를 모스 이론으로 구성할 수 있다. 이 구성을 모스 호몰로지라고 한다.

정의

모스 지표

$M$이 매끄러운 다양체라고 하고, 그 위에 매끄러운 함수 $f:M\to ℝ$이 있다고 하자. $f$의 임계점들은 $f$의 기울기가 0인 $M$의 부분 집합이다. 이를

$\mathrm{Crit}(f)=\{x\in M:\mathrm{d}f=0\in {\mathrm{T}}_x^{*}M\}\subseteq M$

로 표기하자.

$\mathrm{Crit}(f)$에 속하는 $M$의 부분 다양체

$\mathrm{\Sigma }\subseteq \mathrm{Crit}(f)\subseteq M$

가 주어졌다고 하자. 그렇다면, $M$의 접다발을 어떤 임의의 리만 계량을 사용하여 $\mathrm{\Sigma }$ 위에서 접다발과 법다발로 분해할 수 있다.

$\mathrm{T}M\upharpoonright \mathrm{\Sigma }=\mathrm{T}\mathrm{\Sigma }\oplus {\mathrm{N}}_M\mathrm{\Sigma }$

(물론, 만약 $\mathrm{\Sigma }=\{x\}$가 한원소 공간일 경우, $\mathrm{T}\mathrm{\Sigma }=0$이며 $\mathrm{T}M\upharpoonright \mathrm{\Sigma }={\mathrm{N}}_M\mathrm{\Sigma }$이다.)

이 경우, $x\in \mathrm{\Sigma }$ 및 그 근방의 국소 좌표계에 대하여, 헤세 행렬

$({\mathscr{H}}_{x}f{)}_{ij}={\partial }_i{\partial }_{j}f$

을 정의할 수 있으며, 이를 ${\mathrm{N}}_M\mathrm{\Sigma }$에 제한할 수 있다. 이 경우, $f$의 $\mathrm{\Sigma }$에 대한 모스-보트 지표(Morse-Bott指標, 틀:Llang) ${\mathrm{ind}}_f(\mathrm{\Sigma })$는 ${\mathscr{H}}_{x}f\upharpoonright {\mathrm{N}}_M\mathrm{\Sigma }$의 음의 고윳값의 수이다. (이는 사용한 국소 좌표계 및 $x\in \mathrm{\Sigma }$의 선택 및 리만 계량에 의존하지 않는다.) 특히, 만약 $\mathrm{\Sigma }=\{x\}$인 경우, ${\mathrm{ind}}_f(\{x\})$는 단순히 헤세 행렬 ${\mathscr{H}}_{x}f$의 음의 고윳값의 수이다. 이를 ${\mathrm{ind}}_f(x)$라고 쓰며, $f$의 $x$에서의 모스 지표(Morse指標, 틀:Llang)라고 한다.

모스 함수와 모스-보트 함수

매끄러운 함수 $f:M\to ℝ$가 다음 조건들을 만족시킨다면, $f$를 모스-보트 함수(Morse-Bott函數, 틀:Llang)라고 한다.틀:Rp

• $\mathrm{Crit}(f)$는 $M$의 부분 다양체들의 합집합이다. (각 연결 성분들은 서로 다른 차원을 가질 수 있으나, 이들은 맞닿을 수 없다.)
• $\mathrm{Crit}(f)$의 임의의 연결 성분 $\mathrm{\Sigma }$를 골랐을 때, 모든 $x\in \mathrm{\Sigma }$에 대하여 제한된 헤세 행렬 ${\mathscr{H}}_{x}f\upharpoonright {\mathrm{N}}_M\mathrm{\Sigma }$는 비퇴화 쌍선형 형식이다. 이 경우, $\mathrm{\Sigma }$의 모스-보트 지표(Morse-Bott指標, 틀:Llang) ${\mathrm{ind}}_f(\mathrm{\Sigma })$는 ${\mathscr{H}}_{x}f\upharpoonright {\mathrm{N}}_M\mathrm{\Sigma }$의 음의 고윳값의 수이다. (이는 $x\in \mathrm{\Sigma }$에 의존하지 않는다.)

이 경우, 각 ${\mathrm{\Sigma }}_i\subseteq \mathrm{Crit}(f)$를 $f$의 임계 부분 다양체(臨界部分多樣體, 틀:Llang)라고 한다.

또한, 매끄러운 함수 $f:M\to ℝ$에 대하여 다음 두 조건이 서로 동치이며, 이를 만족시키는 함수를 모스 함수라고 한다.

• 모스 함수(Morse函數, 틀:Llang)는 모든 임계점들의 헤세 행렬이 비퇴화 쌍선형 형식인 함수다. 즉, 헤세 행렬이 0을 고윳값으로 갖지 않는다.
• $\mathrm{Crit}(f)$의 모든 연결 성분이 0차원인 모스-보트 함수이다.

성질

모스 함수의 조밀성

매끄러운 함수 $M\to ℝ$의 공간 ${𝒞}^{\mathrm{\infty }}(M,ℝ)$ 위에 임의의 리만 계량을 가해, 다음과 같은 일련의 노름들로 프레셰 공간의 구조를 줄 수 있다.

$\Vert f\Vert {|}_k=\underset{M}{\sup }|f{|}^2+\underset{M}{\sup }\Vert \mathrm{\nabla }f{\Vert }^2+\cdots +\underset{M}{\sup }\Vert {\mathrm{\nabla }}^{k}f{\Vert }^2$

이 프레셰 위상을 ${𝒞}^{\mathrm{\infty }}$ 위상이라고 하고, 이는 사실 사용된 리만 계량에 의존하지 않는다.

이 위상에서, 모스 함수들의 부분 공간은 ${𝒞}^{\mathrm{\infty }}(M,ℝ)$의 조밀 집합을 이룬다.

모스 세포 구조

다음이 주어졌다고 하자.

• 콤팩트 매끄러운 다양체 $M$
• $M$ 위의 모스 함수 $f$

그렇다면, 각 $a\in ℝ$에 대하여 부분 공간

$M^a=f^{-1}(-\mathrm{\infty },a]\subseteq M$

을 정의할 수 있다. 이는 사실 경계다양체를 이룬다.

그렇다면, 임의의 $a,b\in ℝ$, $a<b$에 대하여, 다음이 성립한다.

• 만약 $f^{-1}[a,b]\subseteq M$이 $f$의 임계점을 포함하지 않는다면, $M^a$와 $M^b$는 서로 미분 동형이다.
• 만약 $f^{-1}(a,b)$이 $f$의 임계점 가운데 하나 $x\in M$를 포함하며, 또한 $f^{-1}[a,b]$가 $x$ 이외의 다른 임계점을 포함하지 않는다면, $M^b$는 $M^a$에 $\gamma (x)$차 세포를 추가한 공간과 호모토피 동치이다.

따라서, 만약 서로 다른 두 임계점에 대하여 $f$의 값이 항상 서로 다르다면, $f$는 모스 함수 $f$는 다양체 $M$와 호모토피 동치인 세포 복합체를 결정짓는다. 이 세포 복합체에서 지표가 $k$인 특이점은 $k$차 세포에 대응된다. 또한, 모든 매끄러운 다양체에 대하여 이와 같은 꼴의 모스 함수를 찾을 수 있음을 보일 수 있다.

모스 이론	세포 복합체
모스 함수의 임계점	세포
모스 함수의 임계점의 모스 지표	세포의 차수
$M^a$ ($a$는 임계값이 아님)	$f(x)<a$인 임계점들 $x\in M$에 대응하는 세포들로 구성된 뼈대

모스 부등식

매끄러운 다양체 $M$ 위의 모스-보트 함수 $f$가 주어졌다고 하면, 다음과 같은 모스-보트 다항식(틀:Llang)을 정의할 수 있다.틀:Rp

${\mathrm{MB}}_f(t)=\sum _i{\mathrm{P}}_{{\mathrm{\Sigma }}_i}(t)t^{\gamma ({\mathrm{\Sigma }}_i)}$

이는 물론 모스 다항식의 일반화이다. 만약 $f$가 모스 함수일 경우, 이를 모스 다항식(틀:Llang)이라고 한다.

이제, $M$이 콤팩트 가향 다양체이며, 각 ${\mathrm{\Sigma }}_i$ 또한 모두 가향 다양체라고 하자. (만약 $f$가 모스 함수라면, 둘째 조건은 자명하게 성립한다.) 그렇다면, 모스-보트 부등식에 따르면,

${\mathrm{MB}}_f(t)={\mathrm{P}}_M(t)+(1+t)R(t)$

가 되는, 자연수(음이 아닌 정수) 계수의 다항식

$R(t)\in \mathbb{N}[t]$

이 존재한다.틀:Rp

여기서

${\mathrm{P}}_M(t)=\sum _{n=0}^{\mathrm{\infty }}({\dim }_{\mathbb{Q}}{\mathrm{H}}_n(M;\mathbb{Q}))t^n$

는 $M$의 푸앵카레 다항식이다.

특히, 만약 $t=-1$일 경우

${\mathrm{MB}}_f(-1)={\mathrm{P}}_M(-1)=\chi (M)$

이 된다. 여기서 $\chi (M)$은 오일러 지표이다. (만약 $f$가 모스 함수일 때, 이 사실은 세포 복합체의 세포 호몰로지로부터 간단하게 알 수 있다.)

$f$가 모스 함수일 때, 위 다항식을 차수별로 분해하면,

$|\{x\in \mathrm{Crit}(f):\gamma (x)=k\}|\ge {\dim }_{\mathbb{Q}}{\mathrm{H}}_k(M;\mathbb{Q})$

이다. 즉, $k$차 임계점의 수는 $k$차 베티 수의 상계를 이룬다. (이 역시 세포 복합체의 세포 호몰로지로부터 간단하게 알 수 있다.)

예

초구

$n+1$차원 유클리드 공간 속의 표준적 (반지름 1의) $n$차원 초구

${𝕊}^n=\{x=(t_0,t_1,\dots ,t_n)\in {ℝ}^{n+1}:t_0^2+t_1^2+\cdots +t_n^2=1\}$

를 생각하자. 이 경우, 높이 $t_0$는 모스 함수를 이루며, 이는 두 개의 임계점

$x_{\pm }=(\pm 1,0,0,\dots ,0)$

을 가지며, $x_{+}$는 북극, $x_{-}$는 남극에 해당한다. 이 경우, $x_{+}$의 모스 지표는 $n$이며, $x_{-}$의 모스 지표는 0이다. 이로부터 정의되는 세포 복합체 구조는 하나의 0차원 세포(남극) 및 하나의 $n$차원 세포(남극을 제외한 모든 점)으로 구성된다.

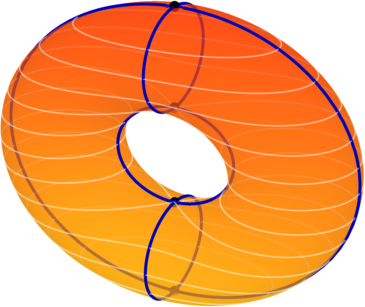
수직 원환면

2차원 원환면 ${𝕋}^2$을 3차원 유클리드 공간에 다음과 같이 매장하였을 때, 높이 함수는 모스 함수를 이룬다.

이는 네 개의 임계점을 가지며, 그 지표는 (아래서부터) 각각 0, 1, 1, 2이다. 이는 원환면의 다음과 같은 세포 복합체 구조를 정의한다. 우선,

${𝕋}^2={𝕊}^1\times {𝕊}^1$

이다. 임의의 두 점 $t,t^{\prime }\in {𝕊}^1$을 골랐을 때,

$e_0=\{(t,t^{\prime })\}$

$e_1=\{t\}\times ({𝕊}^1\setminus \{t^{\prime }\})$

${e_1}^{\prime }=({𝕊}^1\setminus \{t\})\times \{t^{\prime }\}$

$e_2={𝕊}^1\setminus \{t\}\times {𝕊}^1\setminus \{t^{\prime }\}$

는 원환면의 세포 복합체를 정의하며, 이는 위의 모스 함수를 통하여 얻은 것과 동치이다.

보다 일반적으로, 종수 $g$의 콤팩트 가향 곡면 ${\mathrm{\Sigma }}_g$를 위와 같이 배치하자. 그렇다면, 높이 함수는 모스 함수이며, 이는 $2g+2$개의 임계점을 갖는다. 이를 각각 순서대로 $x_1,x_2,\dots ,x_{2g+2}$라고 할 때,

$\gamma (x_1)=0$

$\gamma (x_2)=\cdots =\gamma (x_{2g+1})=1$

$\gamma (x_{2g+2})=2$

이다. 이것이 정의하는 세포 복합체 구조에서, $x_2,\dots ,x_{2g+1}$는 ${\mathrm{H}}_1({\mathrm{\Sigma }}_g)\cong {\mathbb{Z}}^{2g}$의 표준적 기저에 해당한다.

수평 원환면

반대로, 2차원 원환면을 3차원 유클리드 공간 속에서, xy 평면에 회전 대칭을 갖도록 매장하자. 이 경우, z방향 높이는 모스 함수를 이루지 못하지만, 모스-보트 함수를 이룬다. 이 경우 두 개의 임계 부분 다양체 $C_{\pm }$가 존재한다. 이 경우

• $C_{-}$는 “남극”에 있는 원이며, 그 모스-보트 지표는 0이다.
• $C_{+}$는 “북극”에 있는 원이며, 그 모스-보트 지표는 1이다.

원의 푸앵카레 대항식은

${\mathrm{P}}_{{𝕊}^1}(t)=1+t$

이므로, 이 모스-보트 함수의 모스-보트 다항식은

${\mathrm{MB}}_f(t)=(1+t)+(1+t)t=(1+t{)}^2$

이다. 원환면의 푸앵카레 다항식은

${\mathrm{P}}_{{𝕋}^2}(t)=({\mathrm{P}}_{{𝕊}^1}(t){)}^2=(1+t{)}^2$

이므로, 이 경우 모스-보트 부등식이 포화된다 (즉, $R(t)=0$이다).

모스 함수가 아닌 함수

1차원 이상의 매끄러운 다양체 위에서, 상수 함수를 생각하자. 이 경우 모든 점이 임계점이며, 모든 임계점의 헤세 행렬은 0이다. 그러므로 이는 모스 함수가 되지 못한다. (그러나 0차원 다양체(즉, 이산 공간)의 경우 이는 모스 함수를 이룬다.)

임의의 다양체 $M$, $N$ 및 $M$ 위의 함수 $f$에 대하여, $M\times N$ 위에 $f\circ {\mathrm{proj}}_M:M\times N\to ℝ$를 정의할 수 있다. 만약 $N$이 1차원 이상이라면, 이는 항상 모스 함수가 아니다. 그러나 만약 $f$가 모스 함수라면 $f\circ {\mathrm{proj}}_M$는 모스-보트 함수를 이룬다.

역사와 어원

마스턴 모스 이전에도 이미 아서 케일리와 제임스 클러크 맥스웰 등이 측량학에 관련하여, 곡면 위에 정의된 높이 함수의 특이점들을 고려하였다.

마스턴 모스가 변분법을 연구하면서 모스 이론을 1934년 도입하였다. 이후 모스는 평생을 주로 모스 이론을 연구하는 데 바쳤다.

이후 스티븐 스메일 · 라울 보트 · 에드워드 위튼 등이 모스 이론에 공헌하였다.

외부 링크

• 틀:Eom
• 틀:Eom
• 틀:Eom
• 틀:Eom
• 틀:Eom
• 틀:매스월드
• 틀:매스월드
• 틀:Nlab
• 틀:Nlab