틀:위키데이터 속성 추적
틀:미적분학
미적분학에서 삼각 치환(三角置換, 틀:Llang)은 변수를 삼각 함수로 치환하여 적분하는 기법이다.
정의
삼각 치환은 다음과 같은 꼴의 함수의 적분을 구하는 데 사용된다.[1]틀:Rp
여기서 는 유리 함수이며 이다. 이는 의 완전 제곱꼴의 분류이다. 삼각 치환은 를 새 변수에 대한 삼각 함수(의 상수배)로 치환한 뒤 삼각 항등식을 통해 제곱근식을 소거한다. 각 경우에 사용되는 치환은 다음과 같다.[2]틀:Rp[3]틀:Rp
| 적분
|
치환
|
항등식
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
새 변수 의 범위를 각각 아크사인, 아크탄젠트, 아크시컨트의 치역으로 정한 것은 각 치환을 단사로 만들기 위함이다.[2]틀:Rp 쌍곡 치환은 삼각 치환 대신에 쓰일 수 있다.[1]틀:Rp[4]틀:Rp
예
이 들어간 적분
 에 대한 삼각 함수를 다시 로 나타낼 때 이 삼각형을 사용할 수 있다.
에 대한 삼각 함수를 다시 로 나타낼 때 이 삼각형을 사용할 수 있다.
다음과 같은 적분을 구하자.[3]틀:Rp[5]틀:Rp
여기서 이다. 다음과 같은 삼각 치환을 사용하자.
그러면 다음을 얻는다.
|
|
|
(치환)
|
|
|
|
(단순화)
|
|
|
|
(적분)
|
|
|
|
(재치환)
|
이 적분은 와 같은 치환과 아크사인의 도함수를 통해서도 구할 수 있다. 위와 똑같은 삼각 치환을 통해 다음과 같은 적분을 구할 수 있다.[5]틀:Rp
|
|
|
(치환)
|
|
|
|
(삼각 항등식)
|
|
|
|
(적분)
|
|
|
|
(삼각 항등식)
|
|
|
|
(재치환)
|
|
|
|
(단순화)
|
이 적분은 부분 적분을 통해서도 구할 수 있다.
이 들어간 적분
 에 대한 삼각 함수를 다시 로 나타낼 때 이 삼각형을 사용할 수 있다.
에 대한 삼각 함수를 다시 로 나타낼 때 이 삼각형을 사용할 수 있다.
다음을 구하자.[3]틀:Rp
여기서 이다. 다음을 사용하자.
그러면 다음을 얻는다.
|
|
|
(치환)
|
|
|
|
(단순화)
|
|
|
|
(적분)
|
|
|
|
(재치환)
|
이 적분은 치환 및 아크탄젠트의 도함수를 통해서도 구할 수 있다. 위와 똑같은 삼각 치환을 통해 다음과 같은 적분을 구할 수 있다.[5]틀:Rp
|
|
|
(치환)
|
|
|
|
(단순화)
|
|
|
|
(변형)
|
|
|
|
(치환)
|
|
|
|
(적분)
|
|
|
|
(삼각 항등식)
|
|
|
|
(삼각 항등식)
|
|
|
|
(재치환)
|
|
|
|
(적분 상수 재정의)
|
이 적분은 쌍곡 치환 을 통해서도 구할 수 있다.
이 들어간 적분
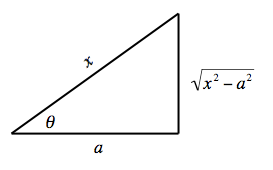 에 대한 삼각 함수를 다시 로 나타낼 때 이 삼각형을 사용할 수 있다.
에 대한 삼각 함수를 다시 로 나타낼 때 이 삼각형을 사용할 수 있다.
편의상 이라고 하고 다음을 구하자.[3]틀:Rp
여기서 이다. 다음을 사용하자.
그러면 다음을 얻는다.
|
|
|
(치환)
|
|
|
|
(단순화)
|
|
|
|
(적분)
|
|
|
|
(재치환)
|
이 적분은 치환 및 아크시컨트의 도함수를 통해서도 구할 수 있다. 위와 똑같은 삼각 치환을 통해 다음과 같은 적분을 구할 수 있다.[5]틀:Rp
|
|
|
(치환)
|
|
|
|
(단순화)
|
|
|
|
(적분)
|
|
|
|
(재치환)
|
|
|
|
(적분 상수 재정의)
|
이 적분은 쌍곡 치환 를 통해서도 구할 수 있다.
정적분
다음과 같은 적분을 구하자.[2]틀:Rp
다음을 사용하자.
만약 일 경우 이므로 이며, 만약 일 경우 이므로 이다. 따라서 다음이 성립한다.
같이 보기
각주
틀:각주
외부 링크


