포인팅 벡터

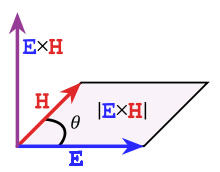
포인팅 벡터(틀:Lang)는 전자기장이 가진 에너지와 운동량을 나타내는 벡터로, 전기장과 자기장의 벡터곱이다.

역사

영국의 존 헨리 포인팅(틀:Lang)이 1883년에 유도하였다.

정의

포인팅 벡터 S는 국제단위계에서 다음과 같다.

$𝐒=\frac{1}{{\mu }_0}𝐄\times 𝐁$

CGS 단위계에서는 $1/{\mu }_0$ 대신 $c/4\pi$를 쓴다.

성질

포인팅 벡터의 크기는 전자기장의 에너지 선속 밀도(틀:Lang, 단위 시간 및 단위 면적 당 에너지)의 크기와 같다. 포인팅 벡터의 방향은 에너지가 전달되는 방향과 같으며 항상 전기장 및 자기장과 수직이다.

전자기장의 운동량과 각운동량

포인팅 벡터는 전자기장의 에너지뿐만 아니라 운동량 $𝐩$와 각운동량 $𝐋$과도 다음과 같이 연관되어 있다.

$𝐩={\mu }_0{ϵ}_0\underset{V}{\int }𝐒d\tau$

$𝐋=𝐫\times 𝐩={\mu }_0{ϵ}_0\underset{V}{\int }(𝐫\times 𝐒)d\tau$

포인팅 정리

포인팅 정리(틀:Lang)는 전자기장을 포함한 계에서의 에너지 보존 법칙이다. 즉, 전자기장이 한 일의 양은 전자기장이 잃게 되는 에너지의 양과 같다는 정리다. 식으로 쓰면 다음과 같다.

$\frac{dW}{dt}=-\frac{d}{dt}\underset{V}{\int }\frac{1}{2}({ϵ}_0{E}^2+\frac{1}{{\mu }_0}{B}^2)d\tau -\frac{1}{{\mu }_0}{\oint }_S(𝐄\times 𝐁)\cdot d𝐚$

우변의 첫 번째 적분은 부피 안에 저장된 전자기장의 에너지이며, 두 번째 적분은 표면의 수직 방향의 전자기파로 방출되는 에너지다. 즉, 포인팅 정리에 따르면, 전자기력에 의하여 전하가 받은 일의 양은 전자기장에 저장된 에너지의 양의 감소량과 표면의 수직 방향의 전자기파로 방출되는 에너지량과 같다.

$\frac{dW}{dt}=\frac{d}{dt}\underset{V}{\int }{u}_{mech}d\tau$

$u_{em}=\frac{1}{2}({ϵ}_0{E}^2+\frac{1}{{\mu }_0}{B}^2)$

역학적 에너지 밀도, 전자기장의 에너지 밀도 식을 이용하여 포인팅 정리 식과 발산정리를 이용하면 포인팅 정리의 미분형을 얻을 수 있다.

$\frac{\partial }{\partial t}(u_{mech}+u_{em})=-\mathrm{\nabla }\cdot 𝐒$