개수로

하천은 대표적인 개수로의 예다. 사진은 한강의 모습

개수로는 수리학에서 관수로와 대비되는 개념으로써, 관로 내 액체가 공기와 접하는 부분, 즉 자유수면이 존재하는 흐름을 말한다.틀:Sfn 개수로 흐름은 중력에 의해 발생한다.틀:Sfn틀:Sfn 자연 하천이나 운하, 물이 꽉 차지 않은 관로 내 흐름 등이 개수로의 예다.틀:Sfn틀:Sfn 개수로에서의 평균 유속은 수면으로부터 총 수심의 60% 깊이에 해당하는 부분의 유속으로 한다.틀:Sfn

용어 정의

• 수심(水深, depth of flow) : 공기와 물이 접하는 자유수면에서 수로 바닥까지의 연직 거리. 중력 방향의 수심을 h, 자유수면에 수직인 수심을 d라고 하면 h cos θ = d이다. 만약 수로 경사 θ가 작다면 $\cos \theta \doteqdot 1$이므로 중력 방향의 수심과 자유수면에 수직인 수심은 같다고 해도 무방하다$(h\doteqdot d)$틀:Sfn틀:Sfn
• 수위(水位, stage) : 자유수면으로부터 임의의 지점까지의 연직 거리를 수위라고 한다.틀:Sfn틀:Sfn 수문학에서는 평균해수면(mean sea level)을 기준으로 하천수표면까지의 높이를 수위라 한다.틀:Sfn
• 수리심, 수리수심(hydraulic depth) 또는 수리평균심(hydraulic mean depth, D) : 수로의 평균 수심을 말하며 유수단면적 A를 수면폭(top width, B)로 나눈 값이다.$(D=\frac{A}{B})$틀:Sfn틀:Sfn틀:Sfn

경심

빨간 부분이 윤변

관이 원형관이 아닌 경우 레이놀즈 수를 구할 때, 즉 $Re=\frac{VD}{\nu }$에서 관의 직경 D값을 대신할 다른 값이 필요하게 된다. 따라서 경심(徑深, hydraulic radius, R) 또는 동수반경틀:Sfn이라는 값을 도입하게 된다.

$R=\frac{A}{P}$

여기서 P는 윤변(潤邊, wetted perimeter)라고 하는데, 관 단면에서 액체가 관 벽에 닿는 부분의 길이를 말한다. A는 유수 단면적이다.틀:Sfn틀:Sfn틀:Sfn틀:Sfn

개수로 단면 유형에 따른 특성값

단면	단면적 A	윤변 P	경심 R	수면폭 B	수리심 D
	bh	b+2h	$\frac{bh}{b+2h}$	b	h
	h(a+b)	$b+\frac{2h}{\sin \alpha }$	$\frac{h(a+b)}{b+\frac{2h}{\sin \alpha }}$	$b+2a$ $=b+2h\cot \alpha$	$\frac{h(a+b)}{b+2a}$ $=\frac{h(a+b)}{b+2h\cot \alpha }$
	$m{h}^2$	$2h\sqrt{1+m^2}$	$\frac{mh}{2\sqrt{1+m^2}}$	2mh	$\frac{h}{2}$
	$\frac{1}{8}(\theta -\sin \theta )D^2$	$\frac{1}{2}\theta D$	$\frac{1}{4}(1-\frac{\sin \theta }{\theta })D$	$(\sin \frac{\theta }{2})D$ $=2\sqrt{h(D-h)}$	$\frac{1}{8}\left(\frac{\theta -\sin \theta }{\sin \frac{\theta }{2}}\right)D$

개수로의 흐름 유형

• 위치에 따른 유속 변화에 따른 분류틀:Sfn틀:Sfn틀:Sfn틀:Sfn틀:Sfn
  • 등류(等流, uniform flow) 또는 균일 유동 : 흐름방향으로 위치에 따라 유속, 수심, 압력 등 흐름 특성 인자가 변하지 않는 일정한 흐름. 이때의 수심을 등류수심(normal depth)라 한다.
  • 부등류(不等流, varied flow or nonuniform flow) 또는 불균일 유동 : 흐름방향으로 위치에 따라 유속, 수심, 압력 등 흐름 특성 인자가 변하는 흐름

• 시간에 따른 유속 변화에 따른 분류틀:Sfn틀:Sfn틀:Sfn틀:Sfn틀:Sfn
  • 정류(정상류, steady flow) : 시간에 따른 유속, 수심, 압력 등 흐름 특성 인자가 변하지 않는 흐름
  • 부정류(비정상류, unsteady flow) : 시간에 따른 유속, 수심, 압력 등 흐름 특성 인자가 변하는 흐름

• 단면 변화 정도에 따른 분류틀:Sfn
  • 점변류(gradually varied flow) : 수면 변화가 완만하게 나타나는 흐름
  • 급변류(rapidly varied flow) : 비교적 짧은 구간에서 급격한 수면 변화를 나타내는 흐름

• 층류, 난류의 구분

개수로의 경우 $Re=\frac{VD}{\nu }=500$을 기준으로 레이놀즈 수가 500 이하이면 층류틀:Sfn, 2000 이상이면 난류, 그 사이는 천이영역으로 구분한다. 이때 D는 관 직경이 아니라 개수로이므로 동수반경 R을 사용한다.틀:Sfn틀:Sfn

비에너지

비에너지(specific energy, h_e)란 기준수평면이 아닌 수로 바닥으로부터 측정된 단위 무게의 물이 가진 에너지이다. 수심을 h, 속도 수두를 $\frac{V^2}{2g}$이라고 한다면 다음 식과 같이 정의한다.

$E=h+\frac{V^2}{2g}$

이것을 가로축이 비에너지, 세로축이 수심인 그래프로 나타낼 수 있다.

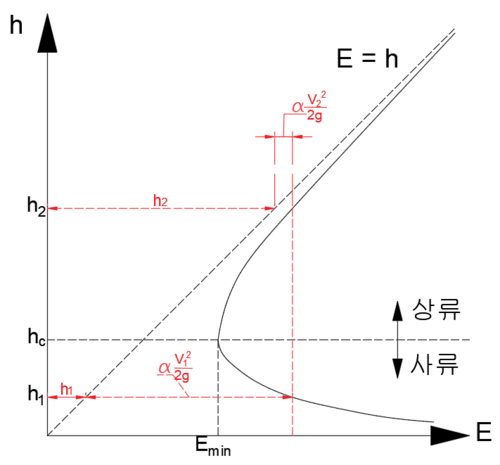
Q=AV이고, Q가 일정할 때 $A=a{h}^n$으로 나타낼 수 있으므로 비에너지는

$E=h+\frac{Q^2}{2g{a}^2{h}^{2n}}$이다.

a는 단면형에 따라 결정되는 상수이다.

하나의 비에너지에 대하여 수심은 2개가 있다. 이 둘을 대응 수심(alternate depths)이라 한다(h₁, h₂) 비에너지가 최소인 경우에는 하나의 수심만이 존재하는데, 이를 한계수심(限界水深, critical depth, h_c)이라 한다. 한계수심보다 큰 수심(h₂)의 흐름은 상류(常流, subcritical flow)라 하고 한계수심보다 작은 수심(h₁)의 흐름은 사류(射流, supercritical flow)라 한다.틀:Sfn틀:Sfn틀:Sfn

비에너지 E가 일정하다고 하고 유량 Q에 관해 식을 정리하면

$Q=\sqrt{2g(E-h)a^2{h}^{2n}}$이고, 한계수심일 때(h=h_c) 유량 Q가 최대가 되며, h=0, E일 때 Q=0임을 알 수 있다. 이것을 그래프로 나타내면 아래와 같다.틀:Sfn

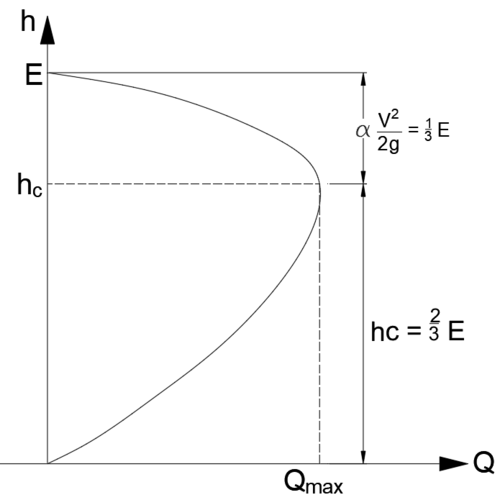
폭이 b인 직사각형 단면에서 한계수심 h_c와 비에너지 E의 관계를 구한다면 그래프 상에서 Q_max인 점에서의 수심이 한계수심 h_c이므로 $\frac{dQ}{dh}=0$이어야 한다. 이를 계산하면 직사각형 단면에서의 한계수심 - 비에너지 관계가 나온다.틀:Sfn

$h_c=\frac{2}{3}E$

$E=\frac{3}{2}{h}_c$

틀:-비에너지를 활용한다면 개수로 수중에 보를 설치하거나, 준설을 하는 경우 수심이 어떻게 될 것인지 예측할 수 있다. 상류의 흐름에 수중보를 설치하는 경우를 예로 들어보자. 편의상 비에너지의 손실은 없다고 가정한다.

개수로의 1단면의 수심은 h₁이고, 유속은 V₁이다. 이때 1단면의 비에너지를 구한다면

$E_1=h_1+\frac{{V_1}^2}{2g}$

2단면에 높이 z인 수중보를 설치했다. 이때의 수심 h₂는 어떻게 될 것인지 알아보자. 수심 h₂는 증가하여 수면이 높아질 것인가, 반대로 h₂가 감소하여 수면이 낮아질 것인가?

2단면 보 상단으로부터 비에너지 $E_2$를 구하면 $E_2=h_2+\frac{{V_2}^2}{2g}$이다. 그러나 이것은 수로 바닥면이 z만큼 높아진 상태에서의 비에너지이다. 원래의 수로 바닥면과는 z의 높이만큼 비에너지 차이가 날 것이다. 비에너지의 손실은 없다고 하였으므로 1단면과 2단면의 비에너지가 같아야 한다. 이것을 식으로 나타낸다면

$E_1=E_2+z$

이제 그래프 상에서 $E_1$을 찾고, 수심 h₁을 찾은 뒤에, $E_1-z=E_2$를 찾은 뒤 수심 h₂를 찾아보자.(흐름이 상류라고 가정하였으므로 그래프에서 한계수심 위의 수심을 보아야 한다) h₂는 h₁에 비해 감소하였음을 알 수 있다. 즉 상류 흐름에 수중보를 설치하면 보가 있는 부분에서 수위는 감소한다. 같은 방법으로 사류일 때를 확인해보면 반대로 수위가 증가한다.

한계흐름의 조건

한계흐름은 비에너지가 최소일 때를 말한다. 따라서 $\frac{dE}{dh}=0$이어야 한다. $E=h+\frac{V^2}{2g}$에서 Q=AV이므로 $E=h+\frac{Q^2}{2g{A}^2}$이고 이 식을 미분하면 $\frac{dE}{dh}=1+\frac{d}{dh}\left(\frac{Q^2}{2g}\frac{1}{A^2}\right)=1-\frac{Q^2}{g{A}^3}\frac{dA}{dh}=0$이다. 따라서 한계흐름이 될 조건은 다음과 같다.

$\frac{Q^2}{g{A}^3}\frac{dA}{dh}=1$

오른쪽 그림에서 dA = b_tdh이므로 위 식은 수면폭 b_t를 이용해 나타낼 수도 있다.

$\frac{Q^2{b}_t}{g{A}^3}=1$

수리평균심의 정의$(D=\frac{A}{b_t})$를 이용하면 위 식은 다음과 같다.

$\frac{V^2}{gD}=1$

이 식을 속도수두로 변형하면 다음을 얻는다.

$\frac{V^2}{2g}=\frac{D}{2}$

프루드 수를 통해 사류, 상류, 한계류를 구분할 수 있다. 프루드 수 $Fr=\frac{V}{\sqrt{gD}}$이므로, $F{r}^2=\frac{V^2}{gD}$이며 만약 $F{r}^2=\frac{V^2}{gD}=1$이라면 위에서 나온 한계흐름의 조건식과 일치한다. 즉 프루드 수가 1이면 흐름은 한계류이다. 한계류일 때의 수리평균심 D를 D_c으로 표현한다. 프루드 수를 통한 흐름 구분을 정리하면 다음과 같다.틀:Sfn

Fr = 1 : 한계류

Fr < 1 : 상류

Fr > 1 : 사류

한계수심 계산

한계수심이 되는 조건은 $\frac{Q^2}{g{A}^3}\frac{dA}{dh}=1$이다. 여기서 $A=a{h}^n$이고, 이것을 수심 h에 대해 미분하면 다음과 같다.

$\frac{dA}{dh}=na{h}^{n-1}\cdots (1)$

한계수심 조건식에서 $\frac{dA}{dh}=\frac{g{A}^3}{Q^2}$이고, A를 대입하면 $\frac{dA}{dh}=\frac{g{a}^3{h}^{3n}}{Q^2}\cdots (2)$가 된다. (1)과 (2)를 결합하고, 수심 h에 대해 정리하면, 이때의 수심 h가 한계수심 h_c이다.틀:Sfn

$h_c={\left(\frac{n{Q}^2}{g{a}^2}\right)}^{\frac{1}{2n+1}}$

직사각형 단면에서 폭이 b라 할 때 a=b, n=1이다.(A=ab이므로) 따라서 직사각형 단면에서의 한계수심 공식은 다음과 같다. 여기서 q는 단위폭당 유량이다.$(q=\frac{Q}{b})$

$h_c={\left(\frac{Q^2}{g{b}^2}\right)}^{\frac{1}{3}}={\left(\frac{q^2}{g}\right)}^{\frac{1}{3}}$

삼각형 단면에서 사면 경사가 1:z일 때, a=z, n=2이며, 한계수심은 다음과 같다.틀:Sfn

$h_c={\left(\frac{2Q^2}{g{m}^2}\right)}^{\frac{1}{5}}$

같이 보기

• 관수로

참고 문헌

• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용
• 틀:서적 인용