끈의 진동

끈의 진동은 파동의 한 형태이다. 일정하게 진동하는 끈은 소리를 만든다. 특정 음의 진동으로부터 소리는 일정한 음을 만든다. 진동하는 끈은 기타, 피아노, 가야금등과 같은 현악기가 소리를 내는 근본적인 원리이다.

파동

끈에 의한 파동의 전파 속력( $v$ )는 아래 식과 같이 나타내어 지며, 전파속도는 끈의 장력( $T$ )의 제곱근에 비례하고 끈의 선형밀도( $μ$ )의 제곱근에 반비례한다.

$v = \sqrt{\frac{T}{μ}} .$

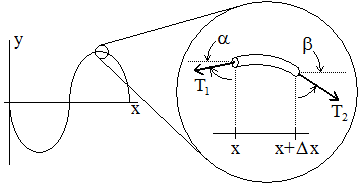
끈의 한지점 x으로부터 작은 $Δ x$ 의 간격을 잡고, $m$ 을 질량, $μ$ 를 선형밀도라고 하자. 끈의 수평축 장력이 $T$ (상수)로서 일정하다고 가정하면, 각 양끝 $x$ 와 $x$ + $Δ x$ 가해지는 장력은 아래와 같이 $T$ 로서 근사할 수 있다.

T_{1 x} = T_{1} \cos (α) \approx T .

T_{2 x} = T_{2} \cos (β) \approx T .

각 양 끝의 끈이 수평축과 이루는 각 $α$ 와 $β$ 가 매우 작다고 생각 하면 수평축의 알짜힘은 0이되어 상쇄된다. 따라서 수직방향의 힘은 전체 알짜힘의 크기와 같음으로 아래와 같이 y에 대한 편미분으로서 표현 할 수 있다.

Σ F_{y} = T_{2 y} - T_{1 y} = T_{2} \sin (β) - T_{1} \sin (α) = Δ m a \approx μ Δ x \frac{\partial^{2} y}{\partial t^{2}} .

양변을 장력 $T$ 으로 나누어 주고 처음에 구했던 $T$ 관한 식을 이용하여 대입하여 주면 아래와 같다.

\frac{μ Δ x}{T} \frac{\partial^{2} y}{\partial t^{2}} = \frac{T_{2} \sin (β)}{T_{2} \cos (β)} - \frac{T_{1} \sin (α)}{T_{1} \cos (α)} = \tan (β) - \tan (α)

각 양끝의 $a$ 와 $b$ 에 대한 탄젠트값이 양끝값의 기울기와 같다는 것을 이용하면 다음과 같이 나타낼 수 있다.

\frac{1}{Δ x} ({\frac{\partial y}{\partial x} |}^{x + Δ x} - {\frac{\partial y}{\partial x} |}^{x}) = \frac{μ}{T} \frac{\partial^{2} y}{\partial t^{2}}

여기서 처음에 $Δ x$ 가 매우 작다고 가정하였음으로 0에 대하여 극한을 취하면 미분의 정의에 의해 $y$ 의 미분값의 미분 즉 $y$ 에 대한 이계미분이 된다.

\frac{\partial^{2} y}{\partial x^{2}} = \frac{μ}{T} \frac{\partial^{2} y}{\partial t^{2}} .

이 식은 $y (x, t)$ 에 대한 파동방정식과 일치한다. 파동방정식에서 시간에 대한 이계미분의 항은 $v^{- 2}$ 와 같다 따라서,

v = \sqrt{\frac{T}{μ}},

$v$ 는 끈에 의한 파동의 전파 속력이다. 하지만, 이 유도는 오직 작은 진폭으로 진동할 때만 유효하다. 큰진폭의 경우에는, $Δ x$ 은 좋은 근사식이 될 수 없다. 수평축의 장력은 상수 $T$ 로서 일정할 필요가 없다.